Geometriemodifikatorgruppe mit Matrix
Dieser Node ist identisch mit der Geometriemodigikationsgruppe, bietet jedoch zusätzlich noch Eingänge für zwei Matrizen.
Durch Nutzung dieser Matrizen lassen sich z. B. globale Punktkoordinaten direkt in lokale Koordinaten eines Objekt umrechnen. Dazu müssen nur die auf das Weltsystem bezogenen Koordinaten mit der invertierten, globalen Matrix des entsprechenden Objekts multipliziert werden.
Ein typischer Anwendungsfall wäre z. B., dass Punkte eines Objekts auf Punktpositionen eines anderen Objekts platziert werden sollen. Da jede Geometrie die eigenen Punktpositionen und auch Normalen lokal, also relativ zum eigenen Bezugssystem speichert, müssen dafür diese Koordinaten umgerechnet werden.
Die Formeln dafür lauten:
lokale Position im Objekt * globaler Matrix des gleichen Objekts = globale Position
und
globale Position * invertierter, globaler Matrix eines Objekts = lokale Position im Objektsystem
In dem nachfolgenden Beispiel wurde so z. B. ein Punkt des Würfels an der Position eines Null-Objekts festgemacht. Sowohl Null-Objekt als auch der Würfel lassen sich weiterhin frei bewegen, ohne dass der fixierte Punkt verrutscht. Wie und ob Sie die Eingänge für lokale und globale Matrix innerhalb der Gruppe nutzen, bleibt Ihnen selbst überlassen.
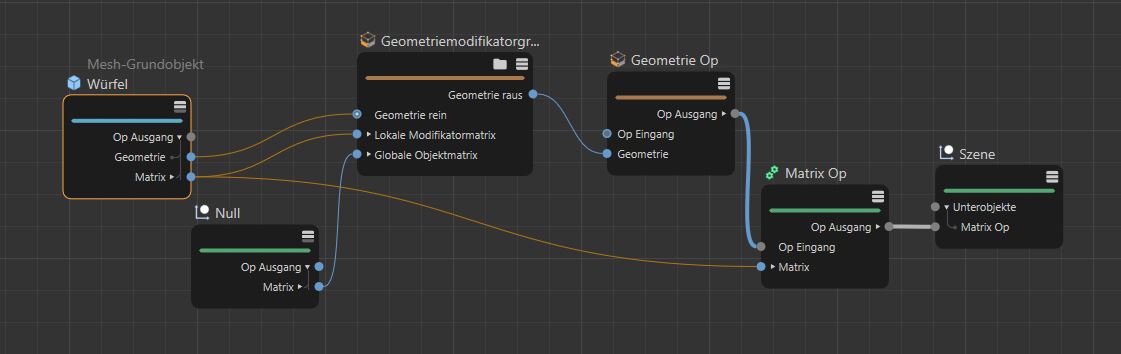Eine Geometriemodifikationsgruppe ermöglicht das Zusammenfassen von Funktionen, die sich mit der Modellierung beschäftigen, was die Wiederverwendung und die Erstellung von Assets vereinfacht. Durch die zusätzlichen Eingänge für Matrizen lassen sich zudem lokale und gloabel Koordinaten einfacher umrechnen.
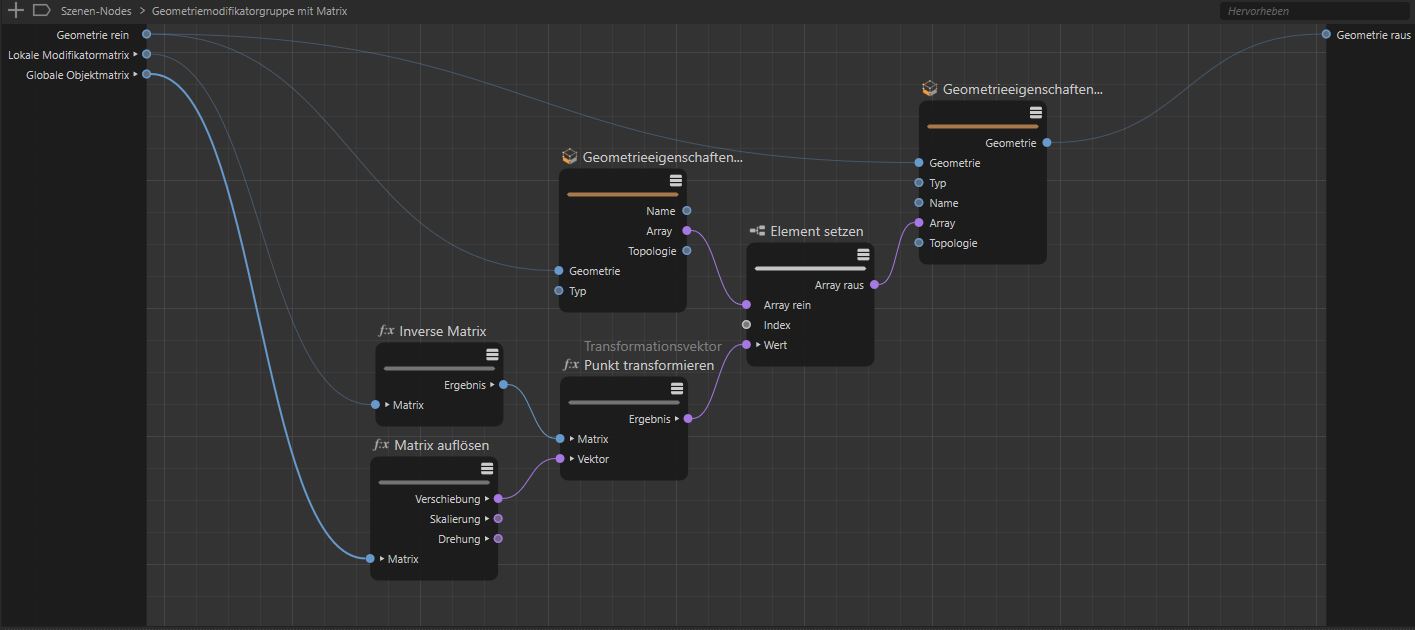In diesem Beispiel wird die Position des Null-Objekts in das lokale Koordinatensystem des Würfel umgerechnet, um einen Würfelpunkt daran zu befestigen.
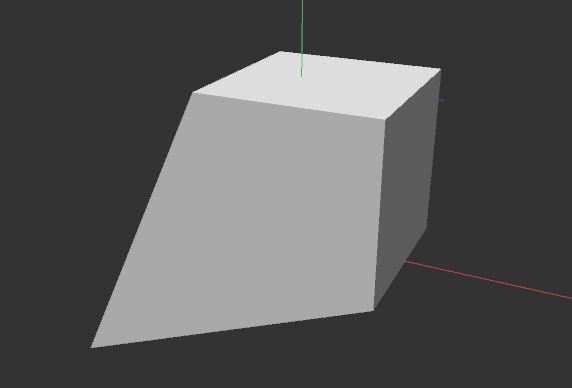Hier ist das Ergebnis zu sehen. Würfel und Null-Objekt sind separate Objekte, aber dennoch bleibt der untere Würfelpunkt fest mit der Position des Null-Objekts verbunden.