Object Properties

Type

With this option you choose the kind of rolling effect you want the curve to adopt.

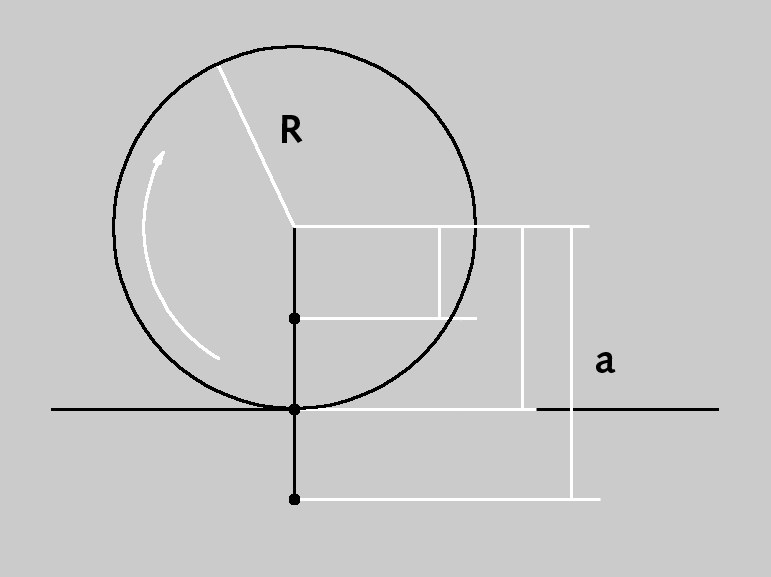Parameters of a basic cycloid object.

Cycloid

The basic cycloid is the rotating curve of a circle (radius R) along a straight line.

Epicycloid

The epicycloid is the rotating curve of a circle (radius r) that moves outside of a second (usually) larger circle (radius R).

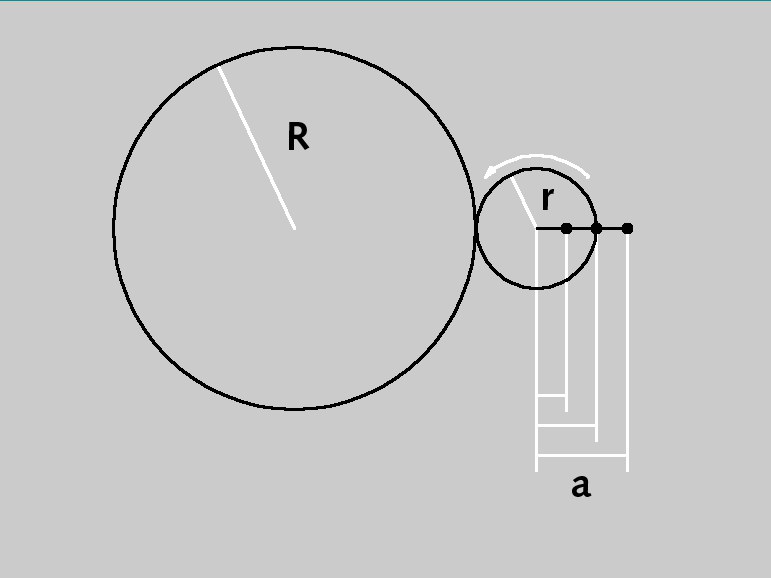Parameters of an epicycloid object.

Hypocycloid

The hypocycloid is the rotating curve of a circle (radius r) that moves inside a second (usually) larger circle (radius R).

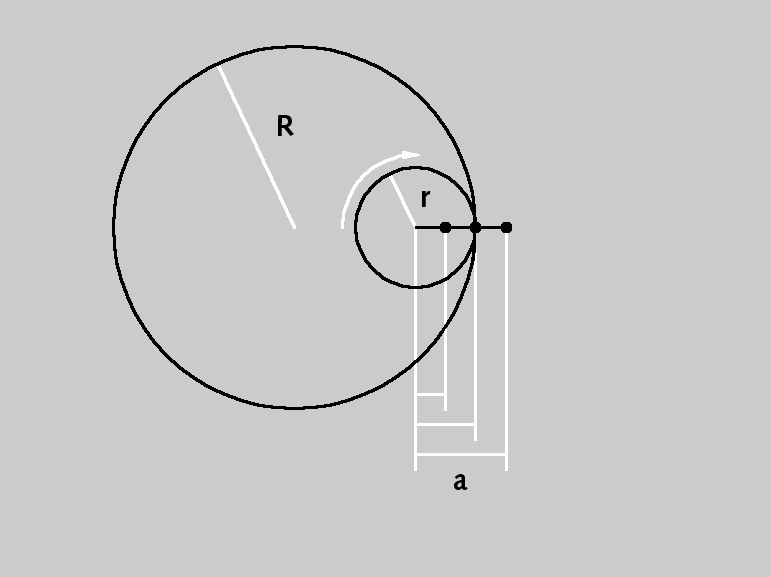Parameters of a hypocycloid.

Radius [0..+∞m]
r [0..+∞m]
a [0..+∞m]

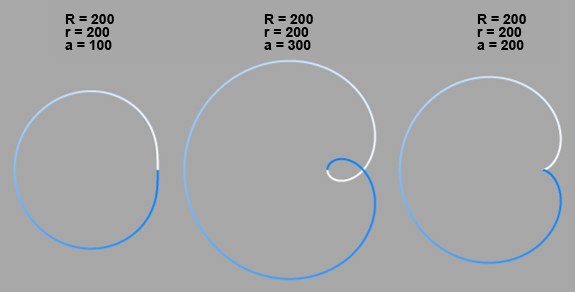
With the basic cycloid (a = R), the observed point P (that the curve forms) is on the radius of the circle. With the shortened cycloid (a < R), it is inside the circle radius, and with the extended (prolate) cycloid (a > R) it is outside.

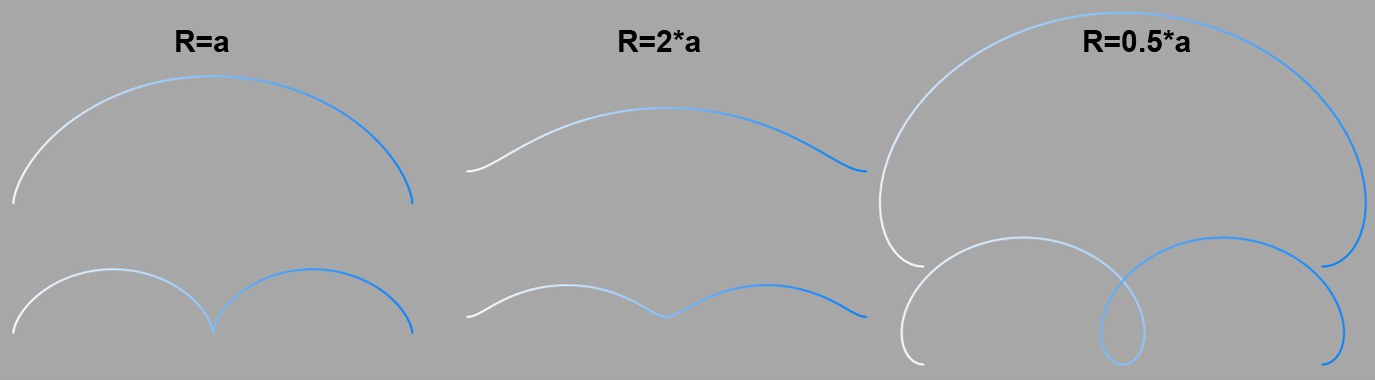: Various r to a relations. Top: Start Angle = 360°; bottom: 720°.

With the basic Epicycloid, the observed point P (that forms the curve) is on the radius of the outer circle (a = r). With the shortened Epicycloid, it is on the inside of the outer circle (a < r), and with the extended Epicycloid it is outside (a > r).

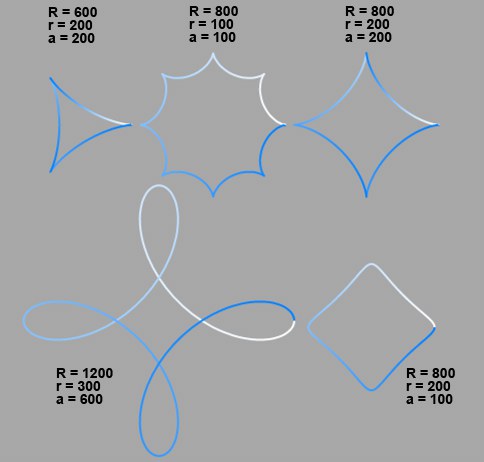
Various Epicyloids

Special cases arise when the both circles are set to the same radius value (known as Pascal’s curve). If, in addition, point P is on the radius of the outer circle (a=r), the result is known as a Cardioid (at right of image).

Epicyloids as limacons.

With the basic Hypocycloid, the observed point P (that forms the curve) is on the radius of the inner circle (a = r). With the shortened Hypocycloid, it is located inside the inner circle (a < r), and with the extended Hypocycloid it is outside (a > r). If the radius of the outer circle is exactly four times the size of the inner circle, the result is an Asteroid (top right of image). The examples below illustrate some of the curves that are possible.

Various Hypocycloids.

Start Angle [-∞..+∞°]
End Angle [-∞..+∞°]

These values define the start and end positions of the rolling circle. There is a small, but crucial, difference between the Cycloid, Hypocycloid and Epicycloid values.

For Cycloid, you simply define the values for the start angle and the end angle of the rotating circle.

With Epicycloid and Hypocycloid, you define the values for the start and end points on the fixed circle. Although the rotating circle still begins at 0°, these angles can be thought of as the range over which the rotating curve becomes visible.

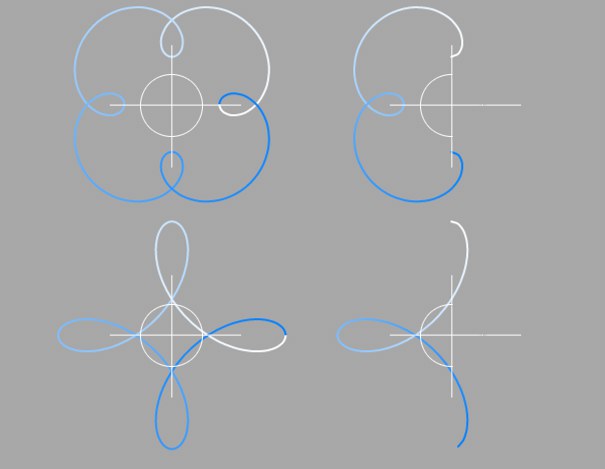Angle range on the left is 0 – 360°, on the right it is 90 – 270°.

Plane

With this drop-down list you choose in which of the three planes the spline primitive is created.

Reverse

Enabling this option will reverse the point order of the spline (see also Spline Primitives.

Intermediate Points

Here you can define how the spline is further subdivided with intermediate points. This affects the number of subdivisions created when using the spline with Generator objects. Even after you select the Interpolation type from the menu for the Intermediate Points, you can still make changes.

None

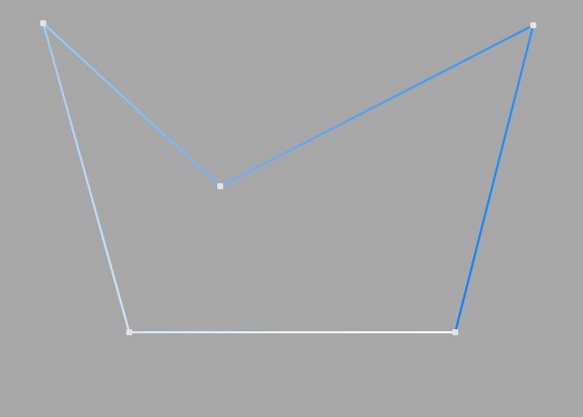
This method of interpolation locates points only at the vertices of a spline, using no additional intermediate points. You cannot enter values into the Number or Angle boxes. For B-splines, the vertices, and therefore points, might not be located on the spline curve.

Natural

This interpolation type first locates points at spline vertices. In the case of B-splines, points are located at positions on the spline curve closest to the spline vertices. Number (N) corresponds to the number of intermediate points between vertices. The points are positioned closer together on areas of the spline with more curvature.

You cannot enter values into the Angle box. The interpolation is not affected by reversing the point order.

Uniform

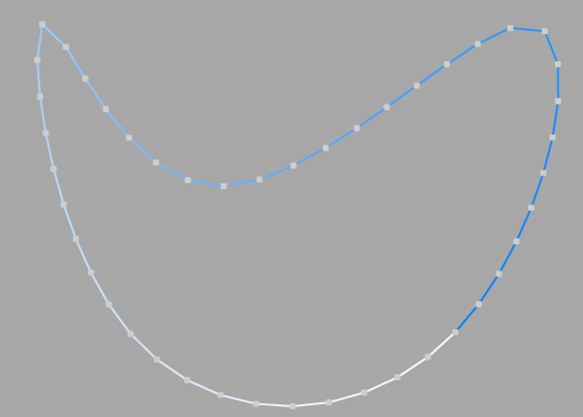
This interpolation subdivides the spline so that the distance between any two consecutive points, as measured along the spline curvature, is constant. One point is always located at the beginning vertex. For open splines, a point is also located at the ending vertex. Other points generally do not coincide with vertices.

You cannot enter values into the Angle box. The interpolation is not affected by reversing the point order.

Adaptive

This interpolation type sets intermediate points whenever the angle deviation of the curve is larger than the value given in Angle. The points of the resulting curve pass through the vertices. If a spline has several segments, then the value of Angle will apply to each segment.

The Adaptive method gives the best results in rendering, hence it is the default interpolation method.

You cannot enter values into the Number box.

Subdivided

Subdivided is similar to Adaptive. Additional intermediate points will be added until the intermediate segments are shorter than the defined Maximum Length, i.e., the point intervals will not necessarily be equal to the maximum length. Lower values will result in higher quality, along with the disadvantages of working with a high number of points - slower refresh times in the editor view, etc.

Especially the render quality of deformed text can be greatly improved using this method. More or less perfect caps and edges without shading errors can be achieved by setting Maximum Length to the same value as Width in the Extrude object (Caps tab, activated Regular Grid option). The subdivision of the letters and caps will match and must not be done manually.

Left: Intermediate points Adaptive; right: Subdivided, applied to an active formula deformation object. Note the defined edges at the right of the image.

Number [0..5000]

Angle [0..90°]

Maximum Length [0.01..+∞m]

This setting controls the maximum spline segment length without adding intermediate points, and is only available if the Intermediate Points parameter is set to Subdivided.