Propiedades del Objeto

Tipo

Con esta opción escoges el tipo de efecto rotacional que quieres que adopte la curva.

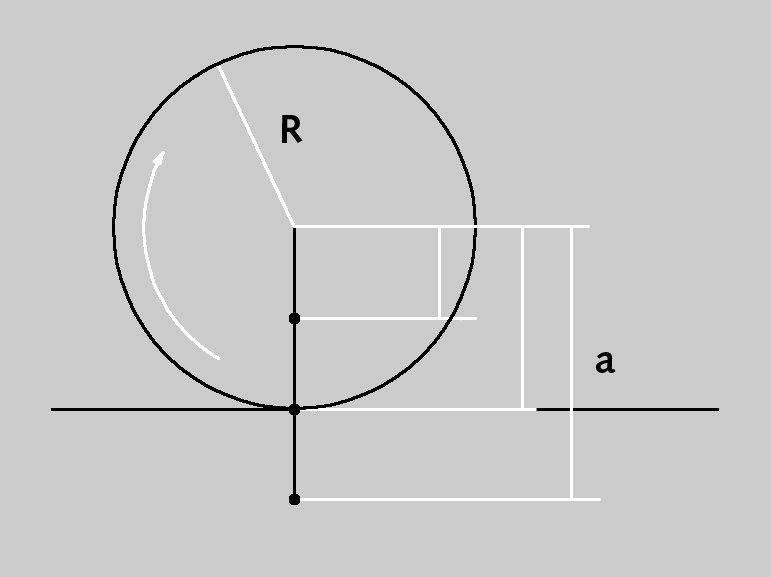Parámetros de un objeto cicloide básico.

Cicloide

El cicloide básico es la curva rotacional de un círculo (radio R) a lo largo de una línea recta.

Epicicloide

El epicicloide es la curva rotacional de un círculo (radio r) que se mueve por el exterior de un segundo circulo generalmente mayor (radio R).

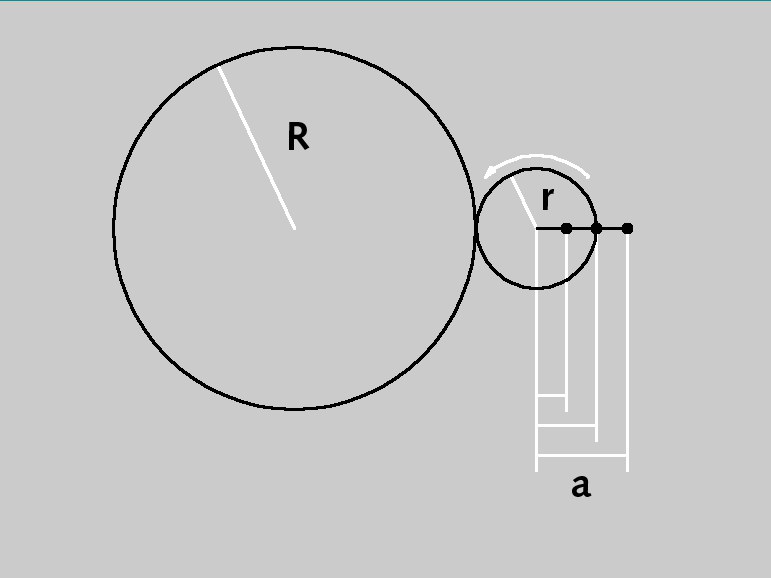Parámetros de un objeto epicicloide.

Hipocicloide

El hipocicloide es la curva rotacional de un círculo (radio r) que se mueve por el interior de un segundo círculo generalmente mayor (radio R).

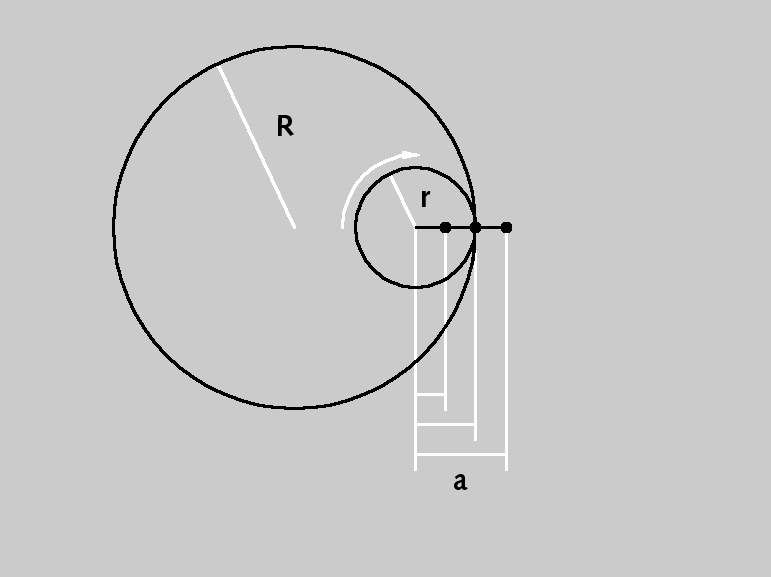Parámetros de un hipocicloide.

Radio [0..+∞m]
r [0..+∞m]
a [0..+∞m]

En el Cicloide básico (a = R), el punto observado (el que forma la curva) está en la circunferencia del círculo. En un cicloide acortado (a < R), está dentro del círculo, y en un cicloide alargado (a > R) está en el exterior.

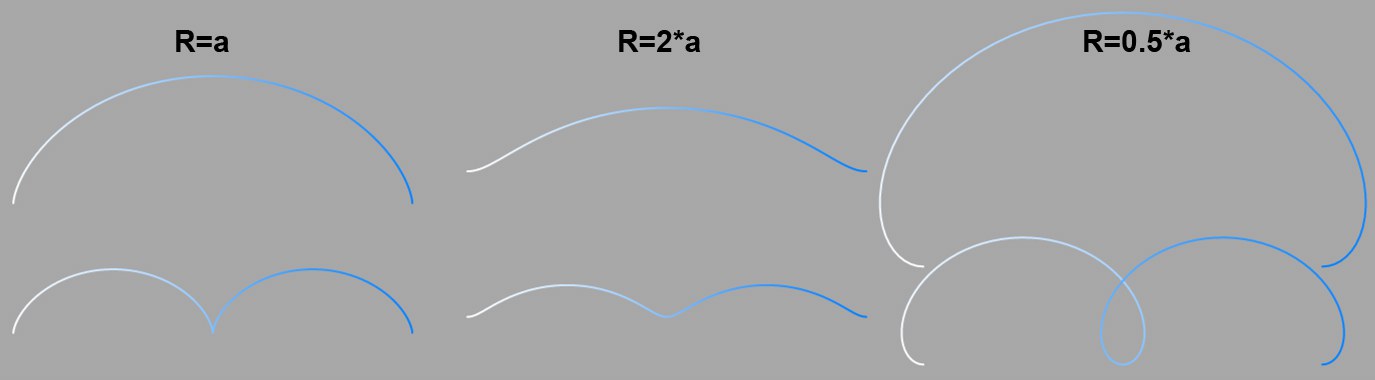: Varias relaciones r - a. Arriba: Ángulo Inicial = 360°; abajo: 720°.

En el epicicloide básico, el punto observado (el que forma la curva) está en la circunferencia del círculo externo (a = r). En un epicicloide acortado, está dentro del círculo externo (a < r), y en un epicicloide alargado está en el exterior (a > r).

Varios Epicicloides

Cuando ambos círculos se configuran con el mismo valor de radio surgen casos especiales (conocidos como curva de Pascal). Si, además, el punto P está sobre la circunferencia del círculo externo, el resultado es conocido como Cardioide (a la derecha de la imagen.)

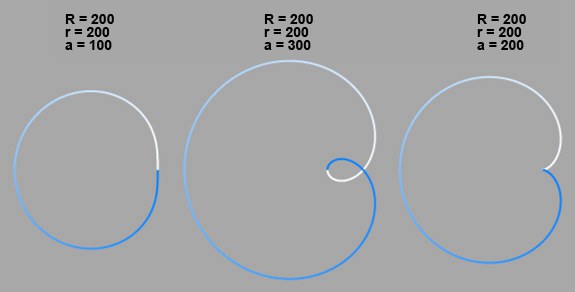Epicicloides como limacones.

En el hipocicloide básico, el punto observado (el que forma la curva) está en la circunferencia del círculo interno (a = r). En un epicicloide acortado, está dentro del círculo interno (a < r), y en un epicicloide alargado está en el exterior (a > r). Si el radio del círculo externo es exactamente cuatro veces el tamaño del círculo interno, el resultado es un Astroide (arriba a la derecha de la imagen). El ejemplo siguiente ilustra alguna de las posibles curvas.

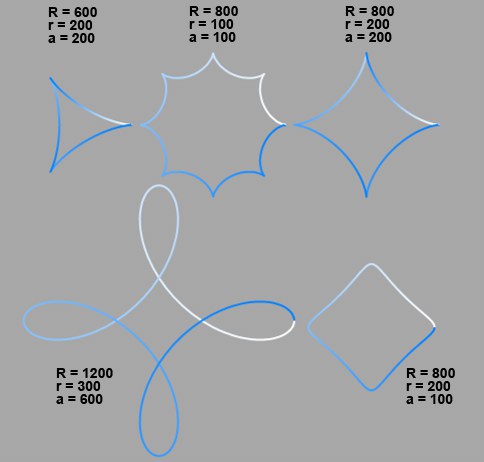Varios Hipocicloides.

Ángulo Inicial [-∞..+∞°]
Ángulo Final [-∞..+∞°]

Estos valores definen las posiciones inicial y final del círculo rotacional. Hay una pequeña pero crucial diferencia entre los valores del Cicloide, Epicicloide e Hipocicloide.

Para los Cicloides, simplemente se definen los valores para los ángulos de comienzo y fin del círculo rotacional.

En los Epicicloide e Hipocicloide, defines los valores de los puntos de inicio y fin en el círculo fijado. Aunque el círculo rotacional comience en 0°, esos ángulos pueden verse como el rango sobre el que la curva rotacional se vuelve visible.

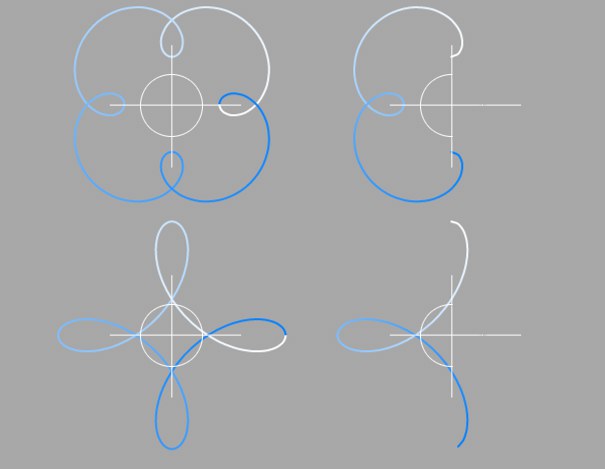El rango del ángulo en la izquierda es de 0 – 360°, en la derecha es de 90 – 270°.

Plano

Con esta lista desplegable puedes elegir en cual de los tres planos se va a crear la primitiva spline.

Invertir

Habilitando esta poción se invertirá el orden de los puntos de la spline (ver también Primitivas Spline).

Puntos Intermedios

Aquí puedes definir cómo la spline es subdividida con puntos intermedios. Esto afecta al número de subdivisiones creadas al utilizar la spline con objetos Generadores. Incluso después de seleccionar el tipo de Interpolación en el menú de los Puntos Intermedios, aún puedes efectuar cambios.

Ninguno

Este método de interpolación localiza puntos sólo en los vértices de una spline, sin utilizar puntos intermedios adicionales. No puede introducir valores en las casillas Número ni Ángulo. Para las B-splines, los vértices, y por tanto, los puntos podrían no estar localizados en la curva spline.

Natural

Este tipo de interpolación localiza primero los puntos en los vértices de la spline. En el caso de B-splines, los puntos están localizados en posiciones de la curva spline lo más cercanos posible a los vértices de la spline. Número (N) corresponde al número de puntos intermedios entre vértices. Los puntos se posicionan lo más cerca posible entre sí en las áreas de la spline con mayor curvatura.

No puedes introducir valores en la casilla Ángulo. La interpolación no se ve afectada por la inversión del orden de puntos.

Uniforme

Esta interpolación subdivide la spline para que la distancia entre dos puntos consecutivos, medida a lo largo de la curvatura de la spline, sea constante. Un punto está siempre localizado en el vértice inicial. En splines abiertas, también se localiza un punto en el vértice final. Otros puntos generalmente no coinciden con los vértices.

No puedes introducir valores en la casilla Ángulo. La interpolación no se ve afectada al invertir el orden de puntos.

Adaptativo

Este tipo de interpolación establece puntos intermedios siempre que el ángulo de desviación de la curva sea superior al valor dado en Ángulo. Los puntos de la curva resultante pasan con precisión a través de los vértices. Si una spline tiene varios segmentos, el valor de Ángulo se aplicará a cada segmento.

El método Adaptable ofrece los mejores resultados de render y, por tanto, es el tipo de interpolación por defecto. Como en los métodos anteriores, no puedes introducir valores en el campo Número.

Subdividido

Subdividido es similar a Adaptable. Se añadirán puntos intermedios hasta que los segmentos sean más cortos que la Longitud máxima, así que los intervalos de puntos no tienen porqué ser necesariamente iguales a la longitud máxima. Valores bajos darán como resultado una calidad mayor, con la desventaja de trabajar con un número mayor de puntos - refresco de vista mas lento en el editor, etc.

La calidad de render de texto deformado puede incrementarse mucho utilizando éste método. Se pueden conseguir tapas y bordes más o menos perfectos y sin errores de sombreado ajustando la Longitud máxima al mismo valor que Anchura en el objeto Extrusión (Pestaña de capas, activando la opción de Cuadrícula Regular). La subdivisión de las letras y las capas se ajustarán y ya no es necesario hacerlo manualmente.

Izquierda: Puntos intermedios Adaptable; derecha: Subdividido, aplicado a un deformador fórmula activo. Fíjate en los bordes definidos a la derecha de la imagen.

Número [0..5000]

Ángulo [0..90°]

Longitud Máxima [0.01..+∞m]

Este ajuste controla la longitud máxima de los segmentos de una spline sin añadir puntos intermedios, y sólo se puede utilizar si el parámetro de Puntos intermedios está ajustado en Subdividido