Koordinaten
Hier finden Sie die Position des Objekts bezogen auf das Welt-System bzw. des Übersystems, falls das Objekt in einer Hierarchie liegen sollte (s.a. Koordinaten-Manager).
Hier finden Sie die Größe des Objekts bezogen auf das Welt-System bzw. des Übersystems, falls das Objekt in einer Hierarchie liegen sollte (s.a. Koordinaten-Manager).
Wenn Sie hier die Größe verändern, entspricht das der Skalierung im Objekt-Modus, es wird also das Achsen-System des Objekts verändert (s.a. Der Unterschied zwischen Objekt- und Modell-Modus).
Hier finden Sie die Winkel des Objekts bezogen auf das Welt-System bzw. des Übersystems, falls das Objekt in einer Hierarchie liegen sollte (s.a. Koordinaten-Manager).
Dieses Auswahlmenü ist nur für die Animatoren unter Ihnen interessant. Es kann die Auswirkungen des gefürchteten "Gimbal Locks" minimieren.
Betrachten Sie sich einmal die folgende Problemstellung:
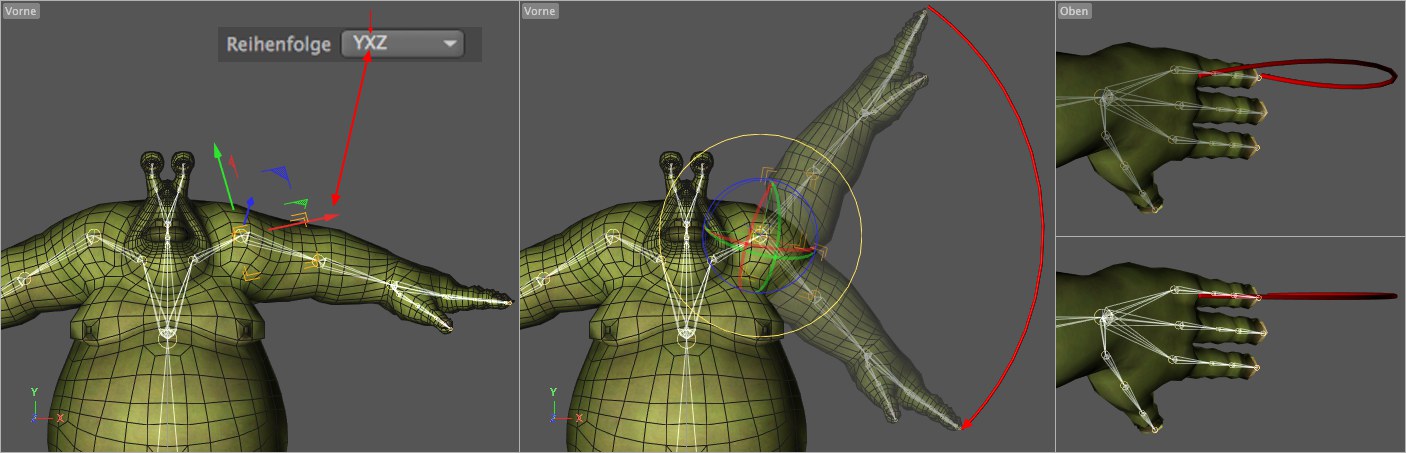
Sie haben hier einen für die Animation vorbereiteten Charakter mit komplexen Hierarchien. Stellen Sie sich jetzt vor, Sie wollen in der Vorderansicht den Schulterjoint des rechten Arms mit einer vermeintlich simplen Drehung von oben nach unten animieren. Erstellen Sie also Keys für einmal Fingerspitzen oben und einmal Fingerspitzen unten. Wenn Sie jetzt die Animation abspielen und von oben auf die Animation blicken, sehen Sie statt der erwarteten ausschließlich senkrechten Drehung einen Schlenker (rechts oben in der Abbildung). Das ist der "Gimbal Lock"-Effekt; hier rel. schwach, kann in Extremfällen aber zu völlig abnormen, korkenzieherartigen Bewegungen führen.
Nun, wie kann die Reihenfolge helfen, diesen Effekt zu minimieren? Dazu müssen Sie nichts weiter tun, als VOR der Animation einen Blick auf die Jointachsen zu werfen und feststellen, um welche der Jointachsen bei der geplanten Animation am wenigsten gedreht wird. In diesem Falle ist das die links markierte X-Achse. Bei Reihenfolge wählen Sie jetzt eine der Optionen, wo die X-Achse an 2. Stelle steht. Wenn Sie jetzt erneut animieren, erhalten Sie eine Bewegung wie rechts unten in der Abbildung zu sehen. Zwar ist ein minimaler, kaum auffälliger Schlenker immer noch zu sehen, allerdings ist das Ergebnis jetzt wesentlich besser als vorher.
Ein weiteres Hilfsmittel zu entscheiden, welche Reihenfolge zu wählen ist, stellt die Option Gimbal-Drehung dar. Aktivieren Sie diese und schalten Sie das Werkzeug Drehen aktiv:
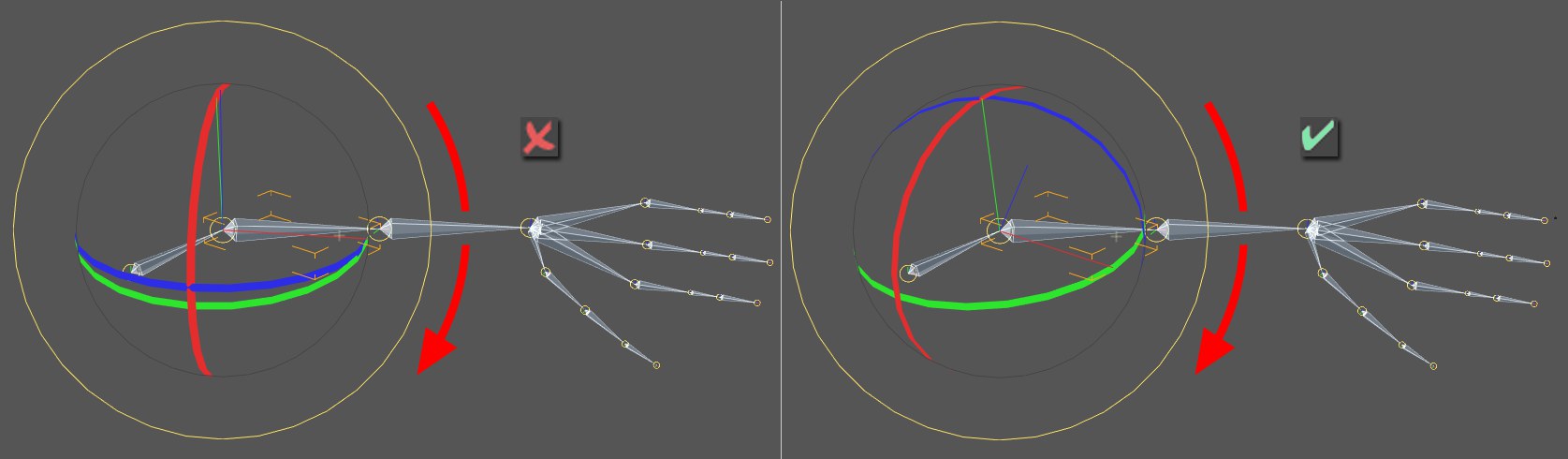 Links Reihenfolge HPB, rechts XYZ.
Links Reihenfolge HPB, rechts XYZ.Hier können Sie direkt anhand der Rotationsbänder (VOR einer Animation) sehen, ob die geplante Animation in einer bestimmten Drehrichtung zum Erfolg führen kann oder nicht. In der Abbildung links sehen Sie die roten, grünen und blauen Rotationsbänder so angeordnet, dass eine Drehung (Roter Pfeil) schon gar nicht möglich scheint (keines der Bänder liegt in der Drehebene). Diese Animation wird Probleme mit dem "Gimbal Lock" bekommen.
Wechseln Sie einfach die Reihenfolge durch, bis eines der Bänder ungefähr in der Drehebene liegt (rechte Abbildung: blau) oder dieser möglichst nahe kommt. Wenn Sie dann animieren, werden Sie wenig Probleme mit dem "Gimbal Lock" bekommen.
Noch ein paar weitergehende Anmerkungen zur Entstehungsweise des Gimbal Lock:
Riskant wird es immer dann, wenn Sie in Abhängigkeit von der Rotationsreihenfolge den jeweils 2., also mittleren Wert (von unten angegebener Markierung) in die Nähe von 90° (bzw. 270°) bringen:
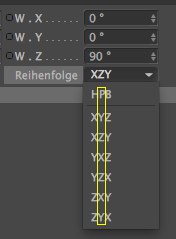
Am besten hat der entsprechende Parameter immer einen minimalen Wert nahe oder gleich 0°.
Traditionell lassen sich diese Problematiken auch durch die Animation eines übergeordneten Nullobjektes umgehen. Hilfreich können ebenfalls die eingefrorenen Selektionen weiter unten im Dialog sein.
![]() Quaternion
Quaternion
Vor Cinema 4D R18 gab es das Quaternion-Tag (dieses erscheint nur noch beim Laden alter Szenen und kann nicht mehr neu erzeugt werden), dessen Funktionalität jetzt als Objekt-Eigenschaft implementiert wurde.
Sicherlich haben Sie schon von dem gefürchteten Gimbal Lock im Zusammenhang z.B. mit Charakter-Animation gehört, bzw. noch schlimmer: Sie haben schon mit ihm zu tun gehabt!
Der Gimbal Lock entsteht, wenn der Winkelwert P +/- 90° aufweist, denn dann haben Heading und Banking, also H und B die gleiche Auswirkung. Das Resultat ist, dass eine Dimension verloren geht und selbst bei kleinen Rotationen große Winkelsprünge erzeugt werden.
Die Quaternion-Funktionalität, die übrigens ausschließlich auf Rotationsanimationen wirkt, bietet Abhilfe!
Standardmäßig benutzt Cinema 4D Euler-Winkel um die Rotation von Objekten zu interpolieren (Euler: Kreiselsystem für entkoppelte Winkel (HPB), Interpolation im euklidischen (rechtwinkl.) 3D-Raum).
Die einzelnen Komponenten der Euler-Winkel werden unabhängig voneinander interpoliert, d.h. der Mittelwert aus HPB (0,0,0) und HPB (60,60,60) wäre z.B. HPB (30,30,30). Dass der Schwenk von 0,0,0 über 30,30,30 nach 60,60,60 nicht unbedingt der kürzest mögliche ist, kann man selbst im Editor ausprobieren.
Gesucht ist also eine Interpolation, welche den KÜRZESTEN Weg von A nach B nimmt, das ist nämlich auch das, was der User manuell machen würde.
Genau diese Randbedingung erfüllen Quaternionen. So geht ein Quaternion von 0,0,0 nach 60,60,60 über 35.104 °,22.83 °,35.104 °!
Damit macht ein Quaternion keine unnötigen Schlenker, und mit anderen Worten: der Gimbal Lock wird vermieden.
Nun werden Sie sich sicherlich fragen, warum man dann nicht gleich ALLEN Objekten prinzipiell eine Quaternion-Animation verpasst. Ganz einfach – wo Vorteile sind, da lauern oftmals auch Nachteile – und so sieht es auch mit der Quaternion Interpolation aus. Solange die Änderungen einer Rotation unterhalb von 180° liegt, kann Quaternion wunderbar arbeiten, darüber hinaus bekommen Sie Probleme, denn wie schon erwähnt, sucht sich das Quaternion den kürzesten Weg.
Der kürzeste Weg für eine Quaternion Expression, ist immer der auf einer 3D Kugel. Man kann sich das ungefähr so vorstellen, dass die Quaternioneninterpolation einer Drehung um eine fixe Achse entspricht. Und zwar der Achse, um die mit dem kleinsten Winkel gedreht werden muss. Diese hat in der Regel mit den Objektachsen nichts zu tun und ist bei jeder Interpolation anders.
Schauen wir uns folgendes Beispiel an:
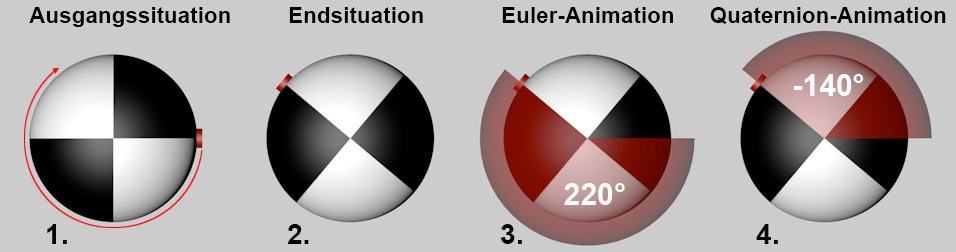
- Eine Objekt soll um eine Achse um mehr als 180° gedreht werden.
- Dazu würden Sie also einen Key für die Ausgangssituation setzen, den Zeitschieber an die Position setzen, an welcher die Rotation beendet sein soll, dann das Objekt nach bewährter Methode nehmen, die entsprechende Rotation einstellen und einen weiteren Key setzen. So weit so gut. Eins schon mal vorweg gesagt, egal ob Sie nun die Quaternion-Funktionalität eingesetzt haben oder nicht, an den beiden Zuständen, also Anfangs- und Endsituation ändert sich absolut nichts! Beide Interpolationsmethoden gehen nur unterschiedliche Wege zum Ziel.
- Schauen wir uns zunächst die althergebrachte Methode von Cinema 4D an, die Drehung per Euler-Winkel:
Sie haben das Objekt per Key (z.B. B, Bank) um 220° gedreht, also dreht sich unser Objekt von der Kameraposition aus gesehen im Uhrzeigersinn um 220°: - Nun zum Verhalten per Quaternion. Wie ja schon definiert, sucht sich diese Interpolationsmethode immer den kürzesten Weg zum Ziel! Der kürzeste Weg hier ist allerdings nicht (vom Betrachter aus gesehen) die Drehung im Uhrzeigersinn um 220°, sondern die genau entgegengesetzter Richtung um nur 140°:
Mit der aktivierten Option Quaternion-Rotation schalten Sie für das entsprechende Objekt die Quaternion-Animation (die Keywerte bleiben identische Euler-Werte, nur die Interpolation zwischen diesen ändert sich) an. Bei deaktivierter Option wird die bekannte Euler-Animation verwendet.
Beachten Sie, dass sich die Quaternion-Interpolation nur auf lokalen Winkelspuren und nicht auf evtl. vorhandene eingefrorene Koordinaten (s. Alles einfrieren) wirkt.
In den Key-Eigeinschaften gibt es eine separate Option Quaternion-Interpolation, mit der Sie die zeitliche Interpolation beeinflussen können.
Folgende Unterschiede zur Euler-Animation ergeben sich:
- in der Zeitleiste werden die Namen der drei Winkelspuren jeweils um ein angehängtes "(Q)" ergänzt, also z.B. "Winkel.P (Q)".
- in der Zeitleiste werden die drei Winkelspuren ("Winkel.H/P/B (Q)") als Einheit angesehen, d.h. bei zeitlicher Verschiebung (oder Erzeugen/Löschen) eines Keys folgen die anderen beiden.
- Key-Tangenten werden von Quaternions nicht unterstützt.
- die Darstellung von Quaternions als F-Kurven ist oft technisch nicht sinnvoll (besonders bei Animationen über 180° zwischen 2 Keys) möglich und ist daher von begrenzter Aussagekraft.
Wann sollten Sie Quaternion-Animationen verwenden und wann nicht?
Greifen Sie auf Quaternion-Animationen zurück:
- wenn Sie Probleme mit Gimbal-Lock und springenden Achsen haben.
Verwenden Sie Quaternion-Animationen NICHT :
- wenn die Winkeldifferenz zwischen 2 Keys 180° überschreitet (es wird immer entlang des kürzesten Weges gedreht).
- wenn Sie F-Kurven feinjustieren (also das "Timing" ändern wollen) wollen.
![]() Eingefrorene Transformation
Eingefrorene Transformation
Zuallererst, Sie werden diese Funktionalität primär nur für Animationen brauchen.
In der 3D-Welt wird das Einfrieren auch "Nullen" (gelegentlich auch "Duale Transformationen" bzw. "Zero Out") genannt. Das ist ziemlich nachvollziehbar, da die lokalen Objektkoordinaten (Position, Größe, Winkel) jeweils auf 0 (Position, Winkel) bzw. 1 (Größe; im Folgenden wird allerdings nur von Position und Winkel die Rede sein) gesetzt werden, ohne dass sich die Position oder Ausrichtung des Objekts ändert.
Den gleichen Effekt hätten Sie, wenn Sie ein Null-Objekt erzeugen, dieses exakt auf die Position und den Winkel des Objekts setzen und das Objekt dem Null-Objekt unterordnen. Tatsächlich wurde diese Methode früher als Workaround verwendet.
Stellen Sie sich dementsprechend das Einfrieren auch so vor: Intern, für Sie unsichtbar wird ein Null-Objekt mit den Koordinaten des aktuellen Objekts eingefügt. Diese Koordinaten werden weiter unten ins Untertab "Eingefrorene Transformationen" kopiert und wirken dann im Folgenden als eine Art Offset zu den Nullkoordinaten, d.h. alles, was in den Hauptkoordinatenfeldern geändert wird, wird mit den eingefrorenen Koordinaten verrechnet.
Nun, wozu soll das gut sein? Dazu muss etwas weiter ausgeholt werden:
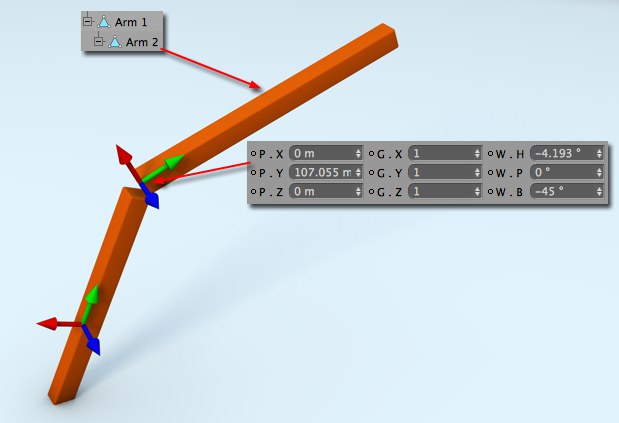
In dieser Szene existieren 2 Objekte: "Arm 2" ist Unterobjekt von "Arm 1" und hat die abgebildeten, lokalen Koordinaten. Die im Attribute-Manager angezeigten Koordinaten sind immer die lokalen (beziehen sich also auf das Koordinatensystem des in der Hierarchie übergeordneten Objekts). So weit so gut.
Sie wollen jetzt "Arm 2" animieren. Er soll sich 45° um seine X-Achse drehen. Üblicherweise drehen Sie an den Rotationsbändern des Objekts und setzen zu verschiedenen Zeitpunkten Keys:
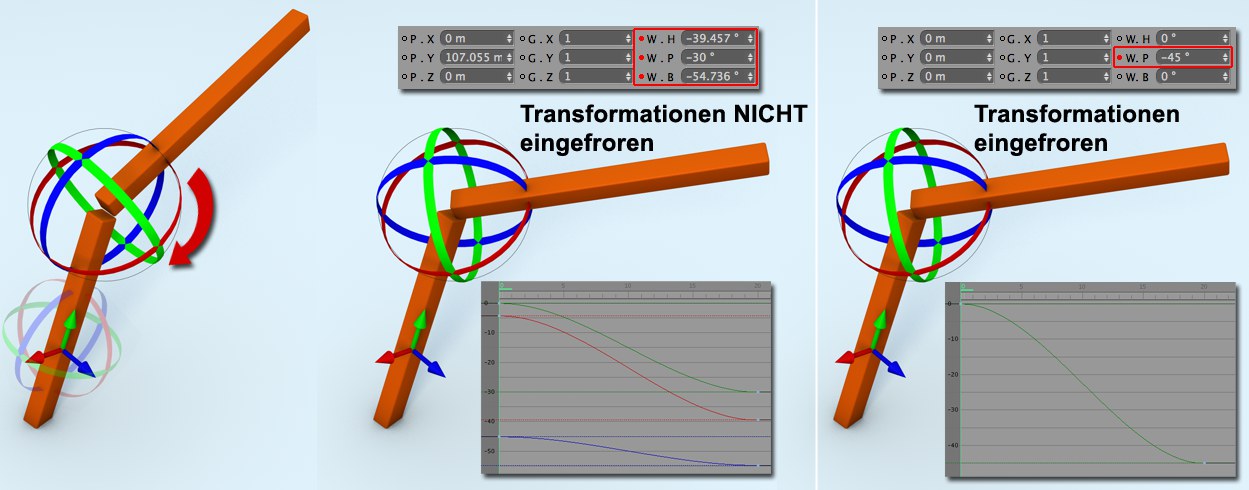
Was dabei passiert, sehen Sie in der Mitte der Abbildung: obwohl nur um eine Achse gedreht wurde, ändern sich alle 3 Winkelkomponenten. Das liegt daran, dass das übergeordnete Koordinatensystem ("Arm 1") gegenüber dem lokalen verdreht ist. Das ist unschön, aber oft nicht zu verhindern. In der Zeitleiste machen 3 evtl. zu bearbeitende F-Kurven die Sache auch nicht gerade leichter. Dazu kommt in diesem Beispiel noch ein Animations-Gimbal-Lock (s. Quaternion-Rotation), der zu einem nichtgeradlinigen Schwenk des Armes führt.
Alle diese Nachteile fallen weg, wenn Sie VOR dem Animieren die Transformationen einfrieren. Damit werden Positions-, Größen- und Winkelwerte jeweils in die darunter angeordneten gleichlautenden Parameterfelder kopiert und die ursprünglichen Werte auf 0 bzw. 1 gesetzt.
Dadurch ergeben sich folgende Vorteile:
- Krumme Koordinatenwerte sind genullt, dadurch können diese leicht auf ihren Ausgangszustand zurückgesetzt werden. Außerdem ist es leichter, z.B. Winkel über XPresso und Slider zu steuern.
- Alle Animations-F-Kurven fangen im Punkt 0 an.
- Bei eindimensionalen Rotationen können Gimbal-Probleme beseitigt werden.
Mit Alles einfrieren frieren Sie sämtliche Koordinaten (Positionen, Größen, Winkel) ein, d.h. alle Hauptkoordinaten werden auf "0" gesetzt.
Es gibt einen separaten Befehl (Hauptmenü: Modus / Koordinaten / Transformationen einfrieren), der dasselbe für alle selektierten Objekte macht.
Die Hauptkoordinaten werden mit den eingefrorenen Koordinaten verrechnet. Danach werden alle eingefrorenen Koordinaten auf "0" gesetzt.
Es gibt einen separaten Befehl (Hauptmenü: Modus / Koordinaten / Eingefrorene Transformationen aufheben), der dasselbe für alle selektierten Objekte macht.
Das hier sind die eingefrorenen Koordinaten, die beim Einfrieren von der übergeordneten Hierarchie übernommen werden.
Die Werte dieser eingefrorenen Koordinaten können Sie in XPresso unter "Koordinaten / Eingefrorene Transformation" im Menü der Ein- und Ausgangsports finden.
Diese Koordinaten können jederzeit hier nach dem Einfrieren geändert werden, wobei die Hauptkoordinaten stets auf "0" stehen bleiben.
P einfrieren
G einfrieren
W einfrieren
Mit diesen Buttons können Sie jeweils separat eine der drei Hauptkoordinaten
- Position
- Größe
- Winkel
einfrieren.
Beachten Sie, dass es beim Einfrieren des Winkels auch zu einer Änderung der eingefrorenen Position kommen kann. Das ist normal und sollte Sie nicht weiter beunruhigen. Denken Sie an ein Überobjekt, wenn dieses gedreht wird (vergleichbar mit einem Einfrieren), muss sich die Position des Unterobjekts ändern, wenn dieses an derselben Position bleiben soll.