MoSpline Básico Coord. Objeto Simple Tortuga Valores Spline Efectos CamposTortuga
Los parámetros en las pestañas Tortuga y Valores están enfocados a usuarios avanzados con experiencia en programación (contienen un L-System completo). No te preocupes si no tienes experiencia en programación. A continuación mostraremos varios ejemplos.
Primero asegúrate de establecer el Modo a
Breve introducción a L-Systems
A continuación se explica brevemente el L(indenmayer)-System. Hay disponibles libros adicionales o recursos online que ofrecen una explicación más profunda de esos sistemas (el documento pdf "The Algorithmic Beauty of Plants" de Przemyslaw Prusinkiewicz y Astrid Lindenmayer puede usarse con Cinema 4D y puede descargarse en http://algorithmicbotany.org/papers#abop).
Los L-Systems normalmente se usan para simular el crecimiento de las plantas y efectos similares. Combinado con MoGraph, pueden usarse para crear espectaculares simulaciones de crecimiento colocando un objeto MoSpline dentro de un objeto Recorrido, creando así un objeto renderizable (las Spines pueden renderizarse directamente usando Sketch and Toon o HAIR).
Dicho de forma sencilla, un L-System ejecuta una serie de comandos que definen cómo y donde deben crecer nuevas ramas. Es un sistema que se produce a sí mismo y que puede reemplazar ramas existentes por otras nuevas.
Los principios básicos son bastante sencillos y están basados en un sistema llamado "Sistema Tortuga (Turtle System)". Se hace "caminar" a una tortuga virtual usando comandos simples. Esta trayectoria se representa por una Spline.
Los 3 comandos más importantes son:
- Una simple F, que simplemente significa "Ve un paso hacia adelante (Forward)". Para una MoSpline significa "Extiende la Spline una unidad (en la dirección Z del objeto)"
- +: Rotar a la derecha
- -: Rotar a la izquierda
Si introduces la secuencia F++F++F en el campo Premisa se traduce a: "Ve un paso hacia adelante; gira dos veces a la derecha; ve otro paso adelante; gira dos veces a la derecha; ve otro paso adelante."
La longitud del paso y la abertura del ángulo de rotación pueden definirse en la pestaña Valores mediante los valores Movimiento por Defecto y Ángulo por Defecto, respectivamente. O, como se describe abajo, colocando esos valores entre paréntesis. Si se define Ángulo por Defecto a 60º se producirá un triángulo perfecto en nuestro ejemplo:
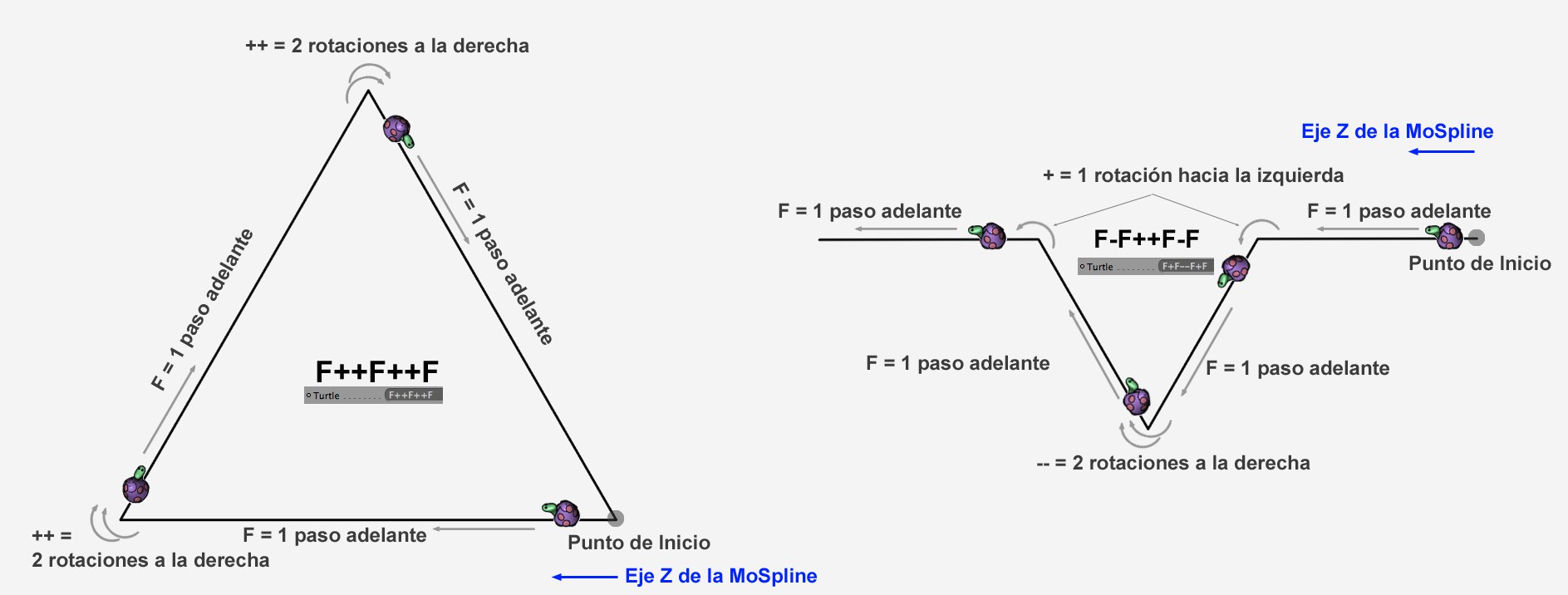Dos códigos de comandos distintos: izquierda F++F++F; derecha: F-F++F-F (cada uno con un Ángulo por Defecto de 60°.Esto permite crear formas tipo ramas. Una función muy interesante de los L-Systems es su sistema de reemplazo integrado con el que pueden reemplazarse ramas individuales por otras. Esto también puede hacerse de forma recursiva, lo que permite crear enramados muy complejos con simples códigos de comandos. Si esto suena confuso, el siguiente ejemplo puede resultar un poco más explicativo:
De momento sólo has introducido líneas de comandos únicas que sólo se ejecutan una vez. Ahora introduce el siguiente código de comandos en los respectivos campos:
Campo Premisa: F++F++F
Campo Normas: F = F-F++F-F
Como puedes ver, la línea de código de Normas contiene una asignación (a partir de ahora lo llamaremos Norma) en la que "F" tiene asignados varios símbolos que de hecho se insertarán (internamente) en la línea de código Premisa.
Si se hubiese escrito de una, la línea de comandos se leería así (reemplaza la F en la línea de código de Premisa con el código que hay después de la "F" en la línea de código de Normas):
F-F++F-F++F-F++F-F++F-F++F-F
Esto representa la segunda forma a la izquierda de la imagen de abajo. Como cada F del código de Premisa se reemplaza por la Norma, cada línea recta se reemplazará por una línea más compleja.
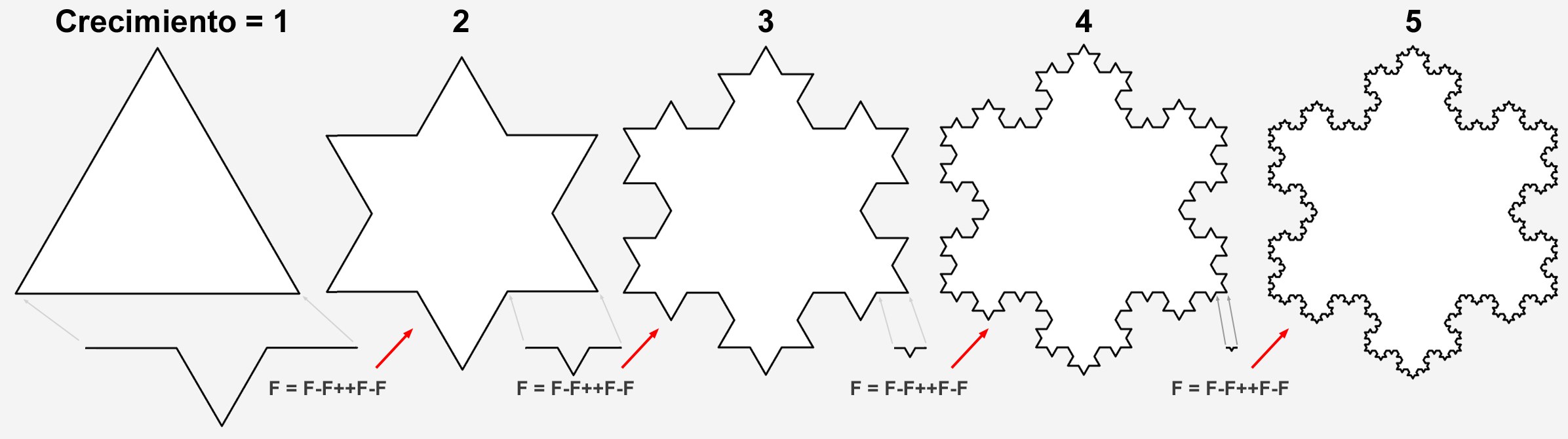Cambia la forma cuando cada F se reemplaza por el código "F-F++F-F".Y este proceso de reemplazo puede repetirse indefinidamente (bueno, no del todo, porque probablemente tu ordenador tirará la toalla cuando la complejidad exponencialmente creciente de las Splines comience a crecer...). El número de veces que este proceso de reemplazo se repite se define por el valor Crecimiento, que reemplaza cada F con el código de Normas. Los fractales funcionan del mismo modo.
Desde luego también pueden usarse marcadores de posición, por lo que no ha de usarse necesariamente cada F. Después de todo, esto sería irreal en formaciones crecientes - el crecimiento longitudinal no siempre se produce sólo al final de la rama, etc.
Para esto puedes usar marcadores de posición (letras que no representan ningún comando Tortuga) como A, B, C, D, (pero NO "F" porque es el comando por defecto "una unidad adelante").
Escribe esto en los campos respectivos:
Premisa: FA
Normas: A=+F-FA
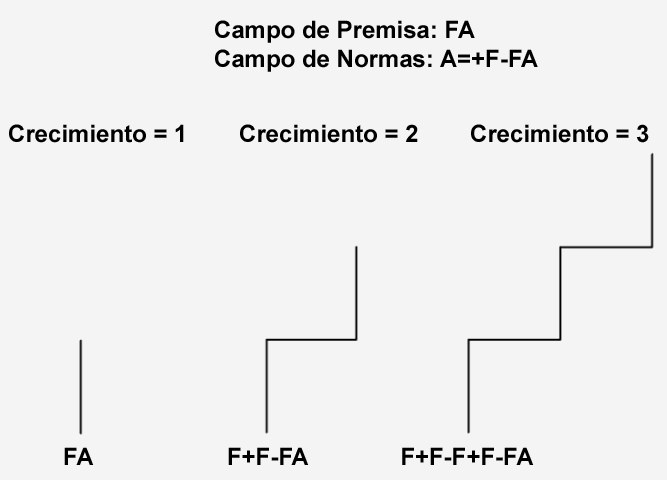
Como la Norma termina con una A, aumentando el valor de Crecimiento hará que la formación crezca indefinidamente (el Ángulo por Defecto está establecido a 90º).
Estas normas de reemplazo en apariencia sencillas pueden crear geometrías increíblemente complejas con varias generaciones (mira abajo). Si se usan los símbolos de forma incorrecta, puedes acabar colgando el ordenador. Por lo tanto ten cuidado al experimentar y guarda el trabajo a menudo (incluso en un simple editor de texto). También es muy útil si estableces Modo Pantalla a
El código que hemos usado hasta ahora ha consistido en una única línea de código ininterrumpida. Sin embargo, cuando los L-Systems se vuelven realmente interesantes es al crear ramas reales, es decir, nuevas líneas que salen de líneas existentes. Y esto puede conseguirse usando corchetes ([ ]). La secuencia de comandos dentro de corchetes es vista como una rama separada (y crea una nueva Tortuga). Una vez se ha creado la rama, la tortuga volverá al punto inicial anterior a los corchetes y continuará con la secuencia de comandos que haya después de los corchetes.
Escribe esto en el campo Premisa:
F[+F][-F[-F]F]F[+F][-F]
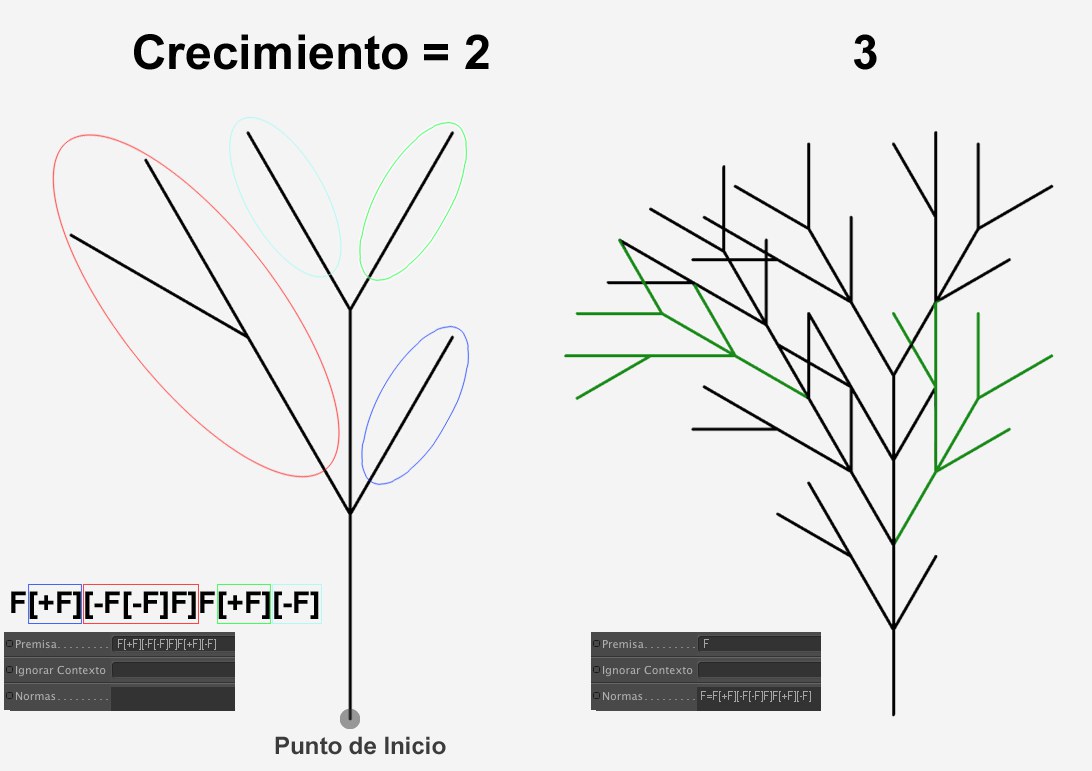Este es el resultado del código de comandos anterior con un Ángulo por Defecto de 30°.Si ahora introduces F en el campo Premisa y el código anterior (F=F[+F][-F[-F]F]F[+F][-F] ) en el campo Normas, cada F se reemplazará por las ramas a la izquierda de la imagen. Aumentando el valor Crecimiento hará que la rama continúe creciendo porque cada línea recta se reemplazará perpetuamente por una nueva rama. Si observas con detenimiento verás que el patrón de la rama a la izquierda se repite en el árbol de la derecha (resaltado en verde).
Este es un modo fácil de crear enramados tipo plantas complejos:
Una serie de símbolos de instrucciones. Tenga en cuenta que cualquier letra (como "A" aquí) se puede utilizar como marcador de posición. En la parte inferior derecha, verá que la rotación predeterminada se estableció en 90 °.Hasta ahora todo lo hemos generado sobre un plano recto. Como los enramados no se producen únicamente en un sólo plano, sino en cualquier dirección, hay símbolos de comandos que hacen esto posible.
Estos son (puede añadirse un valor en grados entre paréntesis después de los símbolos de comandos):
& o ^: rota alrededor del eje transversal de la Tortuga
\ o / : rota alrededor del eje longitudinal de la Tortuga
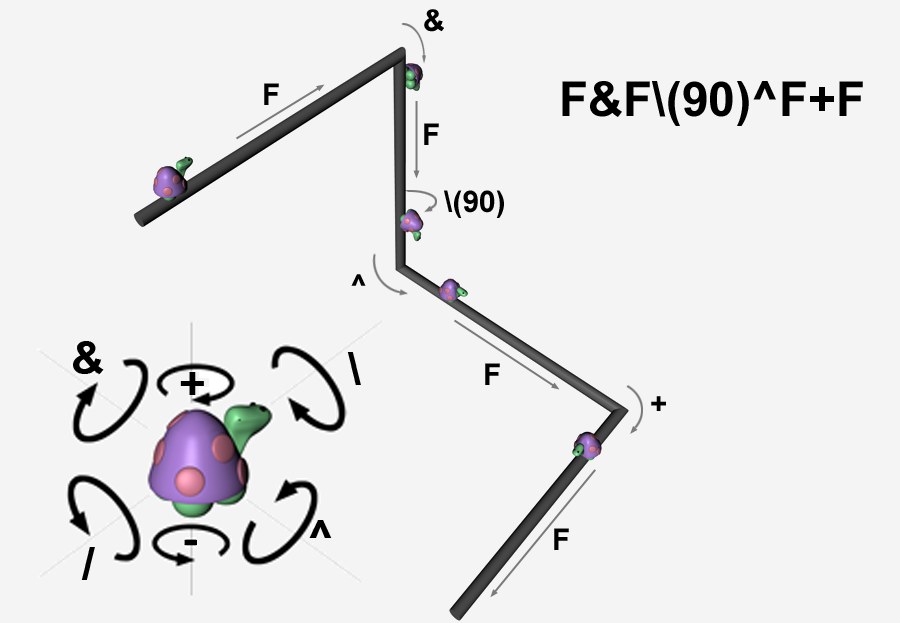
Escribe esto en el campo Premisa: F&F\ (90)^F+F:
El 90º después de "/" no es realmente necesario porque se aplicaría el valor Ángulo por Defecto.El resultado es la Spline mostrada abajo. La tortuga se mueve adelante (F), rota con un ángulo recto alrededor de su eje transversal (&, Ángulo por Defecto a 90º), se mueve hacia adelante otra vez (F), rota 90º alrededor de su eje longitudinal (\ (90), luego 90º alrededor de su eje transversal (^). se mueve otra vez hacia adelante (F), gira a la derecha (+) y finalmente se mueve otra vez hacia adelante (F).
Si usas este método para crear formaciones enramadas espaciales, pueden crearse arbustos y árboles reales.
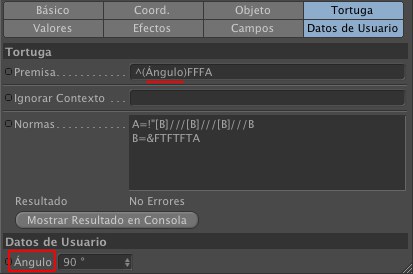
Puedes usar los Datos de Usuario como variables en una secuencia de símbolos. En la imagen anterior se ha añadido un parámetro Ángulo a los Datos de Usuario que luego se ha usado entre paréntesis con ^ (la tortuga rota alrededor del eje transversal) en el campo Premisa.
No incluyas caracteres especiales y espacios en los nombres de variables. Sí se soportan subguiones (p.ej "segunda_longitud") y mayúsculas.
Pueden usarse fórmulas, incluyendo variables definidas (p.ej. F(_growth*2), en vez de dígitos normales. Están disponibles:
| _total | El número total de comandos en la cadena actual (ver más abajo) |
| _index | El índice de comando actual en la cadena (ver más abajo) |
| _growth | El nivel de crecimiento actual. |
| _level | El nivel de comando actual (si está asignado, ver más abajo) |
| _x, _y, _z | La posición actual de la tortuga en el espacio. |
| _arg1, _arg2, _arg3, _arg4 | Los valores de los argumentos primero, segundo, tercero y cuarto (por ejemplo, de F (1,2,3,4)) |
| _age | La edad actual del comando t (representa _growth - _level) comenzando con 0.0. |
| _length | La longitud de arco actual entre los orígenes de Turtle y MoSpline. |
| _move | La longitud de escala predeterminada actual. |
| _tropism | El actual tropismo. |
| _scale | La escala por defecto actual. |
| _rotate | El ángulo por defecto actual. |
| _rnd, random | Un número aleatorio entre -1.0 y +1.0 |
Digamos que tienes la cadena F(_index)F(_index), que consiste en dos comandos. La cadena realiza la misma función que F(1)F(2) (una unidad adelante, luego dos unidades adelante). Por ejemplo, como "_total" es el número total de comandos, puede crearse una espiral con el siguiente comando:
Premisa: FA
Norma: A=+(20*_index/_total)FA
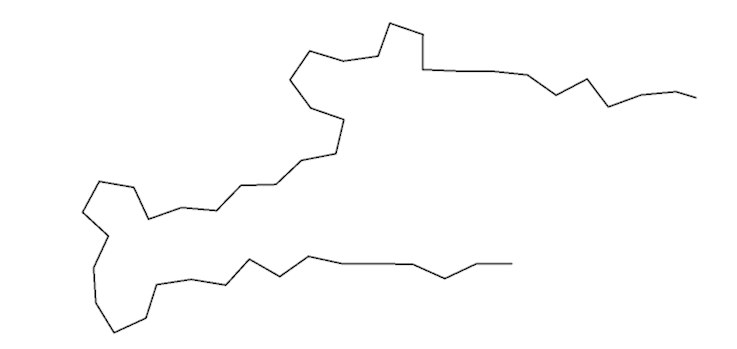
El siguiente comando:
Startstring: A
Regel: A=+(_rnd*90)FA
El comando ,_rnd*90’ determinará un ángulo aleatorio entre -90 y +90 en cada nudo de crecimiento, es decir, producirá una línea ‘temblorosa’ con rotaciones aleatorias.
Digamos que tienes el siguiente comando:
Premisa: A
Norma: A=FA
Se producirán los siguientes valores de nivel (mostrados aquí en paréntesis con propósitos demostrativos - realmente NO se muestran esos valores):
Crecimiento = 0 : A(0)
Crecimiento = 1 : F(1)A(1)
Crecimiento = 2 : F(1)F(2)A(2)
Crecimiento = 3 : F(1)F(2)F(3)A(3)
Ahora que ya sabes cómo se hace la numeración "_index", echa un vistazo al siguiente comando:
Premisa: FA
Norma: A=+F(_level*10)A
...crea la siguiente espiral con Ángulo por Defecto establecido a 90°:
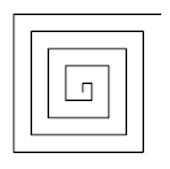
Así como puedes definir F(a,b,c)=F(a*2,b*2,c*2) para establecer parámetros para comandos Tortuga (en este ejemplo F), también puedes usar el comando "_arg". No ha de evaluarse al principio. F=F (_arg1*2,_arg2*2,_arg3*2) hace lo mismo que el comando anterior.
Variaciones avanzadas en la sintaxis
También es posible usar la siguiente sintaxis:
Premisa: F(2)F(1,2)F(2,3)
Norma : F(a,b) = F(a*2,b*2)
Todas las Fs se reemplazarán y donde aparezca "a" o "b" dentro de los argumentos existentes en la F de la Norma, se gestionarán de la siguiente manera:
F(2*2,1*2)F(1*2,2*2)F(2*2,3*2) que lógicamente equivale a F(4,2)F(2,4)F(4,6).
También es posible construir Normas como esta:
F(a,b):(a>10)=F(a,b)+F(a/2)
Esta Norma, por ejemplo, sólo se aplicará si el valor del primer argumento es mayor que 10.
En el siguiente ejemplo se han combinado ambas variaciones en la sintaxis anteriores y producen un efecto interesante:
En este ejemplo, crecen simultáneamente varias ramas. Cuando una rama ha acabado de crecer, se colocará una esfera en el extremo de la rama (requiere el comando J, mira el ejemplo: Objeto Clonar).
Ten en cuenta que "B(6)" se ha definido en la primera Norma y que "B(h-1)" reduce el argumento en 1 en la Norma 2 hasta que "h=0" finalmente establece la esfera en la Norma 3.
Echa un vistazo a la consola para ver toda la cadena (pero primero haz click en el botón Mostrar Resultado en Consola).
Pueden encontrarse más detalles acerca de las fórmulas en el adjunto.
Introduce aquí la premisa. A menudo es un comando formado por una única letra (mira Normas) o un marcador de posición cuyo contenido se añade en el campo Norma. En las siguientes páginas encontrarás numerosos ejemplos del aspecto que pueden tener las cadenas.
Aquí puedes definir una serie de símbolos (comandos) que se ignorarán por las normas contextuales. Ejemplo:
Tienes la siguiente constelación:
Premisa: A+B+C+D+E+F
Normas: A<B=C
| F(a,b,c) | Mueve la tortuga hacia adelante y, opcionalmente, dibuja líneas a lo largo de su longitud (a), para la escala (b) y / o la subdivisión (c). |
| f(a) | Mueve la tortuga hacia adelante y se dibujará la línea NO (es decir, se terminará un segmento Spline) "a" es el valor de longitud opcional. |
| H(a,b,c) | Mueve la tortuga hacia adelante y, opcionalmente, dibuja una línea la mitad del largo de su longitud (a), su escala (b) y / o su subdivisión (c) |
| h(a) | Mueve la tortuga hacia adelante y se dibujará la línea NO (es decir, se terminará un segmento Spline) "a" es el valor de la mitad de la longitud opcional. |
| M(x,y,z) | Mueve y dibuja una línea. La tortuga se moverá dentro de las coordenadas locales (x, y, z) pero no girará. |
| m(x,y,z) | La tortuga avanza pero no dibuja una línea. La tortuga se mueve dentro de las coordenadas locales (x, y, z) pero no girará. |
| G(a) | La tortuga avanza pero no dibuja una línea y no termina un segmento Spline. "a" es el valor de longitud opcional. |
| R | Restablece la Tortuga al punto de inicio del segmento, restablece la rotación y dibuja una línea (en un MoSplineTurtle, un segmento siempre está contenido en / ]). |
| r | Restablece la Tortuga al punto de inicio del segmento, restablece la rotación y no dibuja una línea (en una Tortuga MoSpline, un segmento siempre está contenido en / ]). |
| P(x,y,z) | Coloca la tortuga en estas coordenadas y dibuja una línea.. |
| p(x,y,z) | Coloca a la tortuga en estas coordenadas y no dibuja una línea. |
| -(a) | Gira la tortuga en sentido contrario a las agujas del reloj alrededor del eje vertical. "a" es el valor de ángulo opcional. |
| +(a) | Gira la tortuga en sentido horario alrededor del eje vertical. "a" es el valor de ángulo opcional. |
| &(a) | Gira la tortuga hacia adelante alrededor del eje transversal "a" es el valor de ángulo opcional. |
| ^(a) | Gira la tortuga hacia atrás alrededor del eje transversal. "a" es el valor de ángulo opcional. |
| /(a) | Gira la tortuga en sentido horario alrededor del eje central. "a" es el valor de ángulo opcional. |
| \(a) | Gira la tortuga hacia la izquierda alrededor del eje central. "a" es el valor de ángulo opcional. |
| [ | Nueva rama = nueva tortuga |
| ] | Fin Rama |
| { | Inicio de polígono (ver ejemplo a continuación: "Creación de polígono") |
| } | Fin Polígono |
| . | (Punto: Parada completa) Agrega un punto de polígono, entre paréntesis para polígonos: por ejemplo, = {. -f. + f. + f. + f} |
| | | Gira la tortuga 180 'alrededor del eje vertical. |
| * | Gira la tortuga 180 'alrededor del eje central. |
| % | Pode la rama en este punto: todo se ignorará hasta el final del paréntesis: ] vea el ejemplo "Podar rama". |
| "(a) | Multiplica la longitud por el valor "a" opcional para cada generación (vea el ejemplo a continuación. Ejemplo: Multiplicar / dividir). |
| !(a) | Multiplica la escala por el valor "a" opcional para cada generación (diámetro de MoSpline cuando se usa junto con el objeto de barrido). |
| ;(a) | Multiplica el ángulo por el valor opcional "a" para cada generación. |
| _(a) | Divide la longitud por el valor opcional "a" para cada generación. |
| ?(a) | Divide la escala por el valor opcional "a" para cada generación (diámetro de MoSpline cuando se usa junto con el objeto de barrido). |
| @(a) | Divide el ángulo por el valor opcional "a" para cada generación. |
| T(a) | Agrega Tropismo (por ejemplo, FTFTF), lo que significa que cada segmento Spline se curvará ligeramente en la dirección del eje Y global. Cualquier modificador de partículas presente será evaluado.. |
| $(x,y,z) | Muestra el final de un vector ascendente y orienta a la tortuga en consecuencia. Define un vector en la dirección hacia la cual la tortuga debe enfrentarse. |
| I(a,r,g,b) | (La primera cadena de caracteres comienza con una "i" mayúscula) |
| J(a,r,g,b) | |
| K(a,r,g,b) | |
| L(a,r,g,b) | Para los "I, J, K y L" anteriores, cualquier número de clones generados por un objeto Cloner se puede organizar a lo largo de la Tortuga Spline. "R, g, b" representa el color del clon. "A" es el índice (es decir, el número que representa el orden en el que un objeto está dispuesto debajo de un Cloner. Vea "Índice" a continuación). I, J, K , L representa los grupos respectivos en el parámetro Modo del objeto Cloner, "Grupo 1", "Grupo 2", "Grupo 3", "Grupo 4". A continuación se muestra un ejemplo en "Ejemplo: Objeto Cloner". |
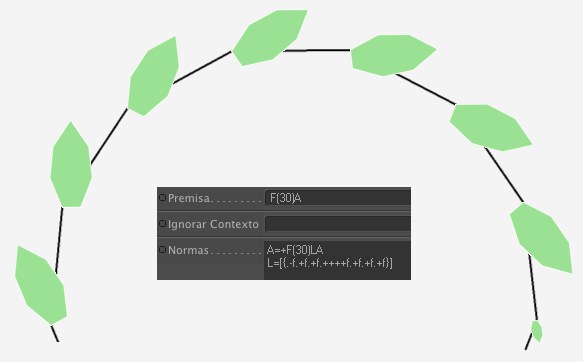
Echa un vistazo a la segunda línea del campo Norma:
L=[{.-f.+f.+f.++++f.+f.+f.+f}]
Entre las llaves (definen un polígono), se ha definido un número específico de puntos poligonales (cada uno comienza con un ".") entre los que se crea un polígono. Como las llaves están dentro de corchetes, la tortuga se restaurará al punto anterior a la creación de la hoja, después de que se haya creado cada hoja.
Toda la hoja se asignará a una "L" y la Norma en la línea anterior creará una hoja completa donde haya una "L".
Ten en cuenta que la MoSpline puede producir o una Spline o un polígono. Si quieres producir ambos simultáneamente, usa Spline de Destino.
Si usas una secuencia de símbolos que se reemplaza a sí misma en el campo Normas (p.ej. A=F+BA), puede usarse un multiplicador o un divisor (", !, ;, _, ?, @) para aumentar o disminuir el valor de cada nuevo Generador.
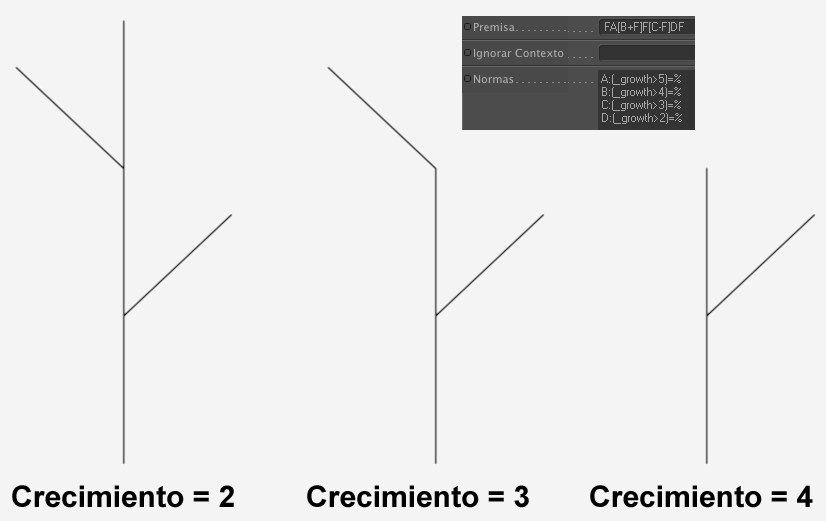
Si echas un vistazo a esta Norma, verás que los marcadores de posición A, B, C y D se han añadido a la premisa. Para varios valores de Crecimiento, las Normas ahora definen el reemplazo de cada marcador de posición con un valor en %, lo que significa que los siguientes símbolos se cortarán en ese punto en (y por) cada rama.
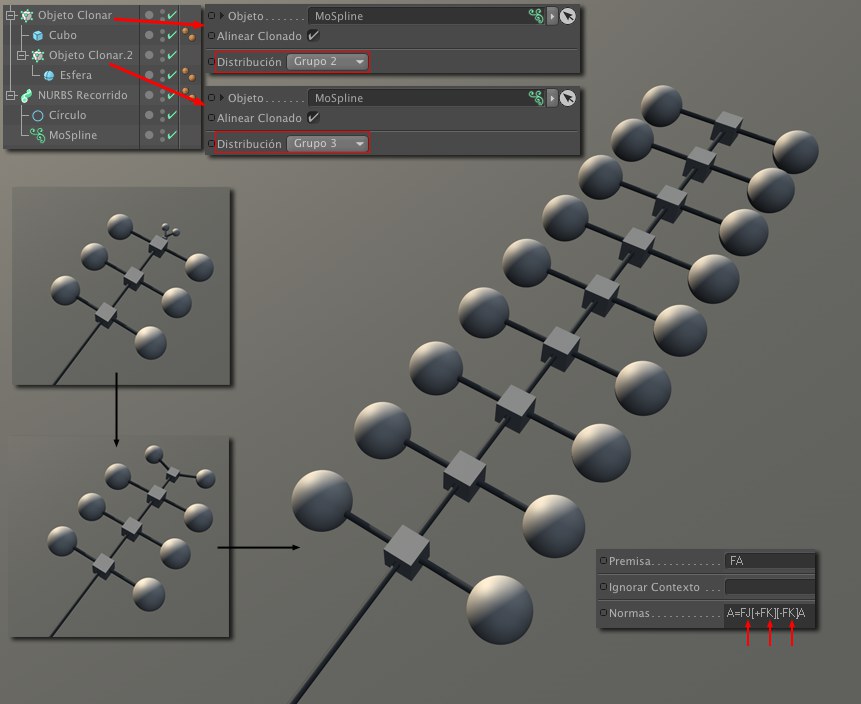Si se anima el valor Crecimiento, esta estructura puede crecer de forma exhuberante (incluyendo clones que crecen).Nota cómo se han usado J y K en la Norma (pueden reemplazarse por (1,1,1,1) y (1,1,1,1), respectivamente, y si se omiten los argumentos entre paréntesis, cada uno usaría el valor estándar) que se refieren a los clones de un objeto Clonar. El modo debe establecerse correspondientemente para ambos objetos Clonar:
I(1,1,1,1) refleja Grupo 1
J(1,1,1,1) refleja Grupo 2
K(1,1,1,1) refleja Grupo 3
L(1,1,1,1) refleja Grupo 4
Ten en cuenta que una Norma
Premisa: FA
Norma: A=FX
X=J(1,1,1,1)
puede funcionar pero los clones crecerán por pasos, mostrándose de forma abrupta.
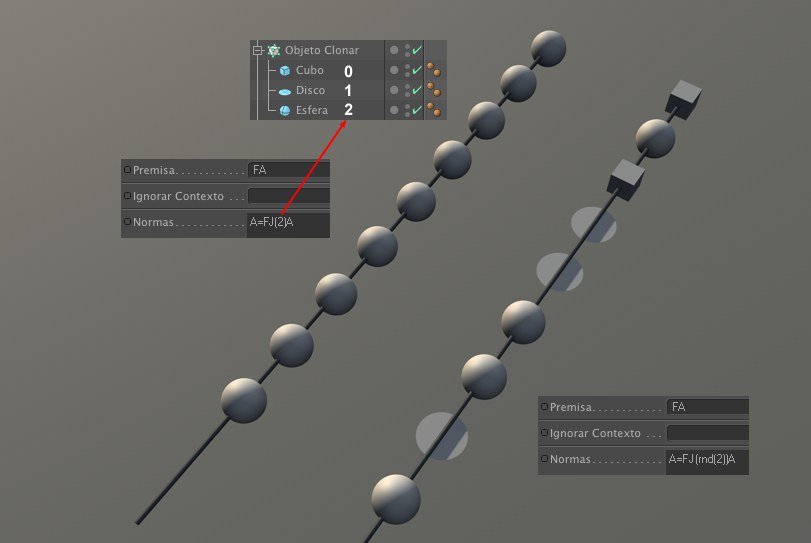
Los objetos Hijo de un objeto Clonar están numerados secuencialmente (comenzando en "0"). Si, por ejemplo, defines A=FJ(2,1,1,1)A (pueden omitirse los valores RGB), el objeto Clonar sólo usará el objeto con el índice "2" (a la izquierda de la esfera). Si usas A=J(rnd(2))A en el lado derecho, se colocará un clon aleatoriamente según un número entre "0" y "2" que también se elige aleatoriamente.
Ejemplo "crecimiento aleatorio"
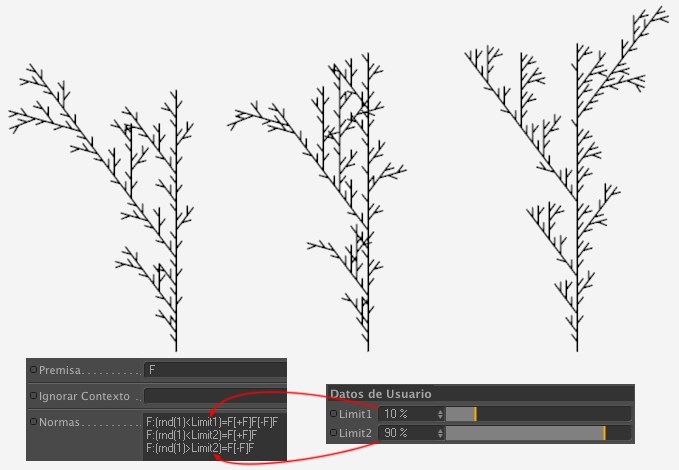Distintos límites generan distintas formas.Esta Norma junto con varios valores de Datos de Usuario como Limit1 y Limit2 (juntos, esos valores equivalen al 100%) pueden usarse para crear "plantas" similares con variaciones (L-System Estocástico). Las condiciones (rnd(1)<) o (rnd(1)>) determinan aleatoriamente cuál de las 3 Normas se aplicará (se hace una nueva selección aleatoria en cada Generación nueva, es decir, con un valor de Crecimiento alto).
Las Normas también pueden escribirse de esta forma:
Premisa: ABC
Norma: A<B=C
Resultado (si Crecimiento > 1): ACC
¿Y qué sucederá?. Eso depende de la secuencia dentro de la cadena resultado. La Norma "A<B=C" busca instancias dentro de la cadena donde una "B" esté justo después de una "A" y reemplaza la "B" por una "C".
Si, por otro lado, introduces "A>B=C", la "A" a la izquierda de una "B" se reemplazará por una "C" (el resultado sería "CBC").
Con la Norma "AB=C" no puede determinarse qué símbolo debe reemplazarse por la "C". En este caso, ambos se reemplazarán por una "C" (el resultado sería "CCC").
Muestra errores de sintaxis.
Haciendo click en este botón se mostrará en la Consola la secuencia de símbolos que está actuando actualmente, teniendo en cuenta todas las Normas y el parámetro Crecimiento. El aspecto de esa secuencia podría ser el siguiente (esta es la secuencia de símbolos del ejemplo de frutas con Crecimiento establecido a 4):
