MoSpline-Objekt: Turtle

Funktion verfügbar in CINEMA 4D Broadcast, Studio

Basis Koord. Objekt Einfach Turtle Werte Spline Effektoren Kräfte

Turtle

Die MoSpline-Einstellungen der Tabs "Turtle" und "Werte" sind für die Fortgeschritteneren unter Ihnen gedacht, die ein wenig Programmiererfahrung mit sich bringen (hinter diesen beiden Tabs verbirgt sich ein komplettes sog. "L-System"). Die nicht so Programmiererfahreneren sollten sich jedoch trotzdem nicht abschrecken lassen. Sie finden auf dieser Seite diverse Beispiele, die Sie variieren können.

Vergessen Sie nicht, Modus zunächst auf Turtle zu stellen.

Kurze Einführung in L-Systeme

Die folgenden Seiten stellen eine kurze Einführung in die sog. "L(indenmayer)-Systeme" dar. Sie finden in der Literatur bzw. im Internet ausführliche Abhandlungen darüber (es sei an dieser Stelle auf das PDF "The Algorithmic Beauty Of Plants" von Przemyslaw Prusinkiewicz und Aristid Lindenmayer verwiesen, was hier http://algorithmicbotany.org/papers#abop herunterladbar ist und an das sich die Cinema 4D-Implementation anlehnt).

L-Systeme werden traditionell vor allem zur Simulation von Pflanzenwachstum und ähnlichen Effekten verwendet. Im Zusammenhang mit MoGraph lassen sich damit spektakuläre Wachstumsanimationen erstellen, indem Sie das MoSpline-Objekt in ein Sweep-Objekt werfen und damit ein renderbares Objekt erschaffen (mit den Funktionalitäten Sketch and Toon bzw. HAIR lassen sich Splines auch direkt rendern).

Vereinfacht gesagt, gibt es in einem L-System eine Abfolge von Anweisungen, die definieren, wie und wo neue Zweige wachsen. Das ganze ist ein selbstreproduzierendes System, das bestehende Zweige durch neue ersetzen kann.

Die Grundlagen sind recht einfach und basieren auf einem sog. "Turtle-System" (Turtle bedeutet im Deutschen Schildkröte). Eine (virtuelle) Schildkröte wird mittels einfacher Anweisungen auf den Weg geschickt. Dieser Weg entspricht dann einem Spline.

Die 3 wichtigsten Anweisungszeichen sind:

ein simples F, was nichts weiter bedeutet als "Gehe einen Schritt vorwärts (Forward)" oder auf den MoSpline übertragen "Verlängere den Spline um eine Einheit" (in Objekt-Z-Richtung).
+: Drehe Dich nach rechts
-: Drehe Dich nach links

Wenn Sie bei Startstring also die Zeichenfolge F++F++F eingeben, bedeutet das im Klartext: (ausgehend von der positiven Z-Achse) "Gehe einen Schritt nach vorne, drehe Dich 2 Mal nach rechts, gehe wieder einen Schritt nach vorne, drehe Dich nochmals 2 Mal nach rechts und noch einmal einen Schritt nach vorne."

Wie groß jeweils der Schritt und der Winkel bei einer Drehung ist, lässt sich im Tab "Werte" mittels Standardwinkel und Standardverschiebung einstellen oder kann auch, wie unten beschrieben, in Klammern gesetzt werden. Wenn Standarddrehung auf 60° steht, erhalten Sie mit dem Beispiel ein perfektes Dreieck:

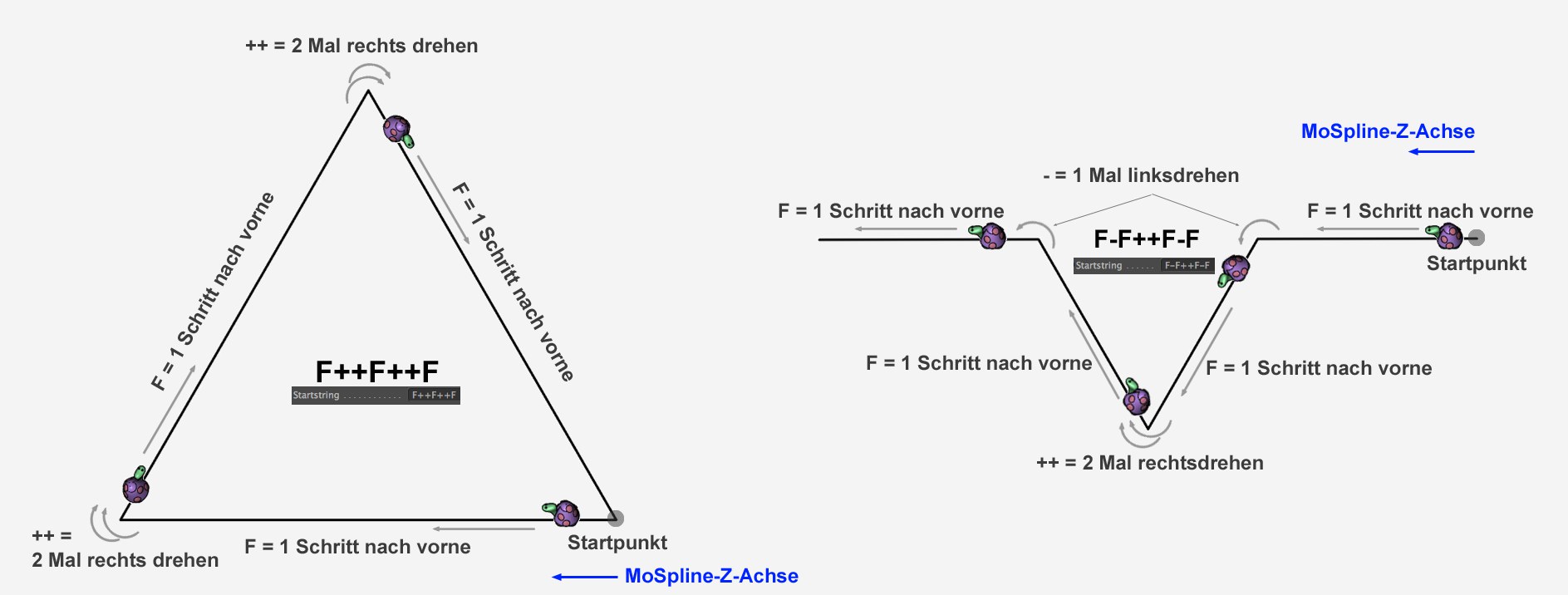Zwei verschiedene Anweisungszeichenfolgen: links "F++F++F" und rechts "F-F++F-F" (beide mit Standardwinkel von 60°).

Auf diese Art und Weise lassen sich Zweigformen erstellen. Der eigentliche Gag von L-Systemen ist jedoch das integrierte Ersetzungssystem, das einzelne Zweige durch andere Zweige ersetzen kann. Das kann auch rekursiv geschehen, was aus einigen simplen Anweisungszeichen komplexeste Verzweigungen erzeugen kann. Wovon erzählt der Autor hier eigentlich? Nun, folgendes Beispiel wird etwas Licht ins Dunkel bringen.

Bisher schrieben Sie einfach einzeilige Anweisungsfolgen, die genau einmal ausgeführt werden. Tippen Sie jetzt einmal folgendes in das Startstringfeld:

Feld Startstring: F++F++F

Feld Regeln: F = F-F++F-F

Wie Sie sehen, steht in der 2. Zeile eine Zuweisung (im folgenden Regel genannt), es wird nämlich dem Zeichen "F" eine ganze Anweisungszeichenfolge zugewiesen, die wiederum (intern) oben in die erste Zeile eingefügt wird.

Ausgeschrieben lautet die Anweisungszeichenfolge (ersetzen Sie die oberen F durch das, was in der 2. Zeile rechts vom "="-Zeichen steht):

F-F++F-F++F-F++F-F++F-F++F-F

Dies entspricht der zweiten Abbildung von links im nächsten Bild. Da jedes F durch die längere Regel der 2. Zeile ersetzt wird, wird jeder gerade Strich durch den komplexeren Linienhaken ersetzt. Die Schildkröte muss also immer längere Wege zurücklegen.

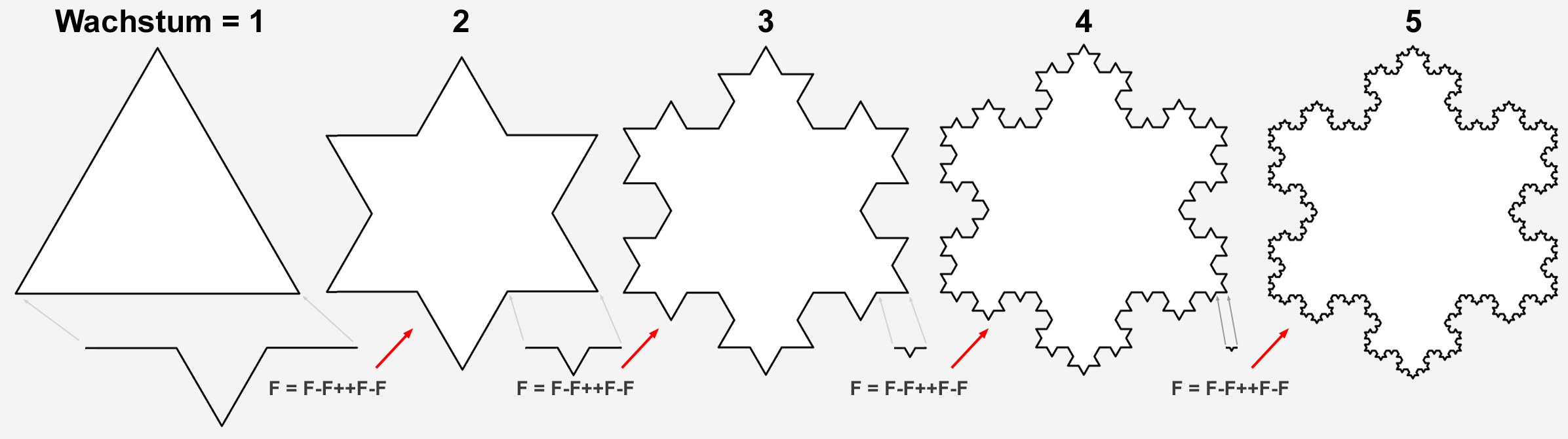Formänderung, wenn jedes F durch "F-F++F-F" ersetzt wird.

Und diesen Ersetzungsvorgang lässt sich prinzipiell beliebig (naja, nicht ganz, Ihr Rechner wird aufgrund der exponentiell ansteigenden Splinekomplexizität bald in die Knie gehen) weit fortführen (wie oft diese Ersetzung vorgenommen wird, definiert das Wachstum), indem jedes "F" wieder durch eine Anweisungszeichenfolge ersetzt wird.

Genauso funktionieren übrigens auch Fraktale.

Natürlich können auch Platzhalter verwendet werden, um nicht zwangsweise jedes "F" ersetzen zu müssen, weil das bei wachsenden Gebilden ja auch nicht der Fall ist, Längenwachstum findet in der Regel ja immer am Ende von Zweigen o.ä. statt.

Dazu können Sie Platzhalter verwenden (Buchstaben, die keinem Turtle-Befehl entsprechen), z.b. A, B, C, D ("F" NICHT, das ist der "eine-Einheit-nach-vorne"-Befehl.)

Tippen Sie einmal folgendes in die beiden Felder

Feld Startstring: FA

Feld Regeln: A=+F-FA

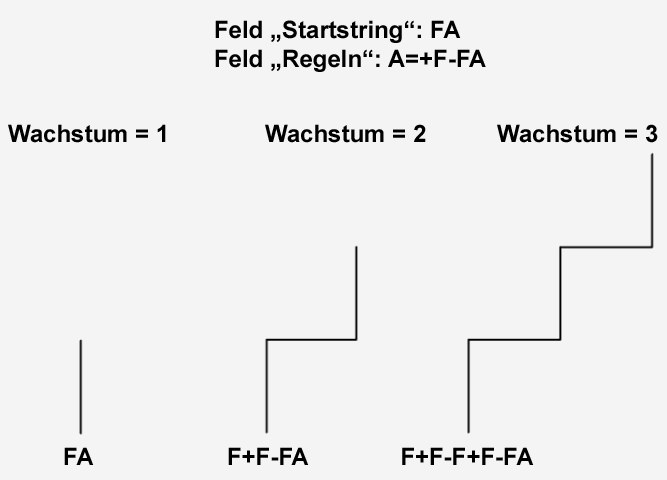
Da hier im Feld "Regeln" A=+F-FA am Ende wieder ein "A" steht, wird die Regel mit anwachsendem Parameter Wachstum immer wieder hinten dran gehängt, d.h. das Gebilde kann endlos wachsen (Standardwinkel hier übrigens 90°).

Hinweis:
Diese simpel aussehenden Ersetzungsregeln können nach mehreren Generationen eine erstaunlich komplexe Geometrie erzeugen (s.u.). Einige unbedacht eingesetzte Zeichen können Ihren Rechner direkt in die Knie zwingen. Seien Sie also vorsichtig beim Herumprobieren und speichern Sie die Zeichenfolgen öfters mal ab (ruhig auch in einem simplen Texteditor). Es ist auch durchaus lohnenwert Anzeigemodus auf Linie zu setzen.

Die bisher erwähnten Formen bestanden ausschließlich aus einer ununterbrochenen Linie. L-Systeme werden aber erst interessant, wenn echte Zweige, d.h. von Linien abzweigende neue Linien erstellt werden können. Und genau das machen Sie mit eckigen Klammern [ ]. Die Anweisungszeichenfolge innerhalb einer eckigen Klammer wird als separater Zweig angesehen (und somit eine neue Turtle erzeugt). Nach dem Ablaufen eines Zweiges wird die Schildköte auf die Ausgangsposition vor der eckigen Klammer zurückkehren und von da aus die Anweisungszeichenfolge nach der eckigen Klammer abarbeiten.

Geben Sie im Startstringfeld einmal folgendes ein:

F[+F][-F[-F]F]F[+F][-F]

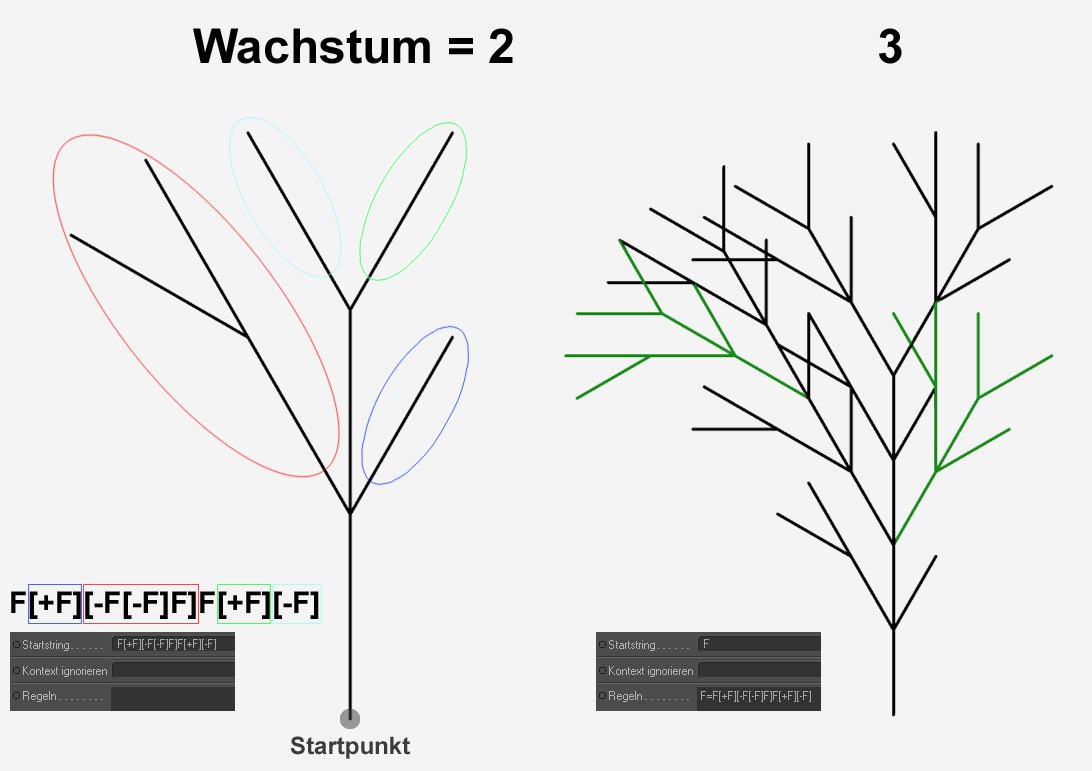Mit der abgebildeten Anweisungszeichenfolgen ergeben sich diese Zweige bei einem Standardwinkel von 30°.

Wenn Sie bei Startstring jetzt F und bei Regel das vorher im Startstringfeld stehende F=F[+F][-F[-F]F]F[+F][-F] (vergessen Sie nicht, ganz vorne ein F= hinzuzufügen) eingeben, wird, genauso, wie oben schon beschrieben, jedes "F" durch den im obigen Bild links abgebildete Zweig ersetzt. Indem Sie Wachstum vergrößern, lassen Sie auch den Zweig immer weiter wachsen, da jede gerade Linie fortwährend durch einen neuen Zweig ersetzt wird. Wenn Sie genau hinsehen, erkennen Sie die linke Aststruktur im rechten Astgebilde immer wieder (grün eingefärbt).

Auf diese Art und Weise lassen sich problemlos aufwendige pflanzenähnliche Verästelungen erzeugen:

Verschiedene Anweisungszeichenfolgen. Beachten Sie, das auch beliebige Buchstaben (wie hier "A") als Platzhalter verwendet werden können. In der rechten (unteren) Abbildung wurde zusätzlich Standarddrehung auf 90° gestellt.

Bis jetzt hat sich alles in der flachen Ebene abgespielt. Da sich die Verästelungen natürlich nicht nur flächig entwickeln können, sondern in der Lage sind, sich in beliebige Winkel auszubreiten, gibt es Anweisungszeichen, die genau dafür verantwortlich sind.

Es sind dies (hinter den Anweisungszeichen kann in Klammern eine Gradzahl angegeben werden):

& bzw. ^: Drehen um die Turtle-Querachse

\ bzw. / : Drehen um die Turtle-Längsachse

Tippen Sie jetzt einmal "F&F\ (90)^F+F" in das Textfeld Startstring:

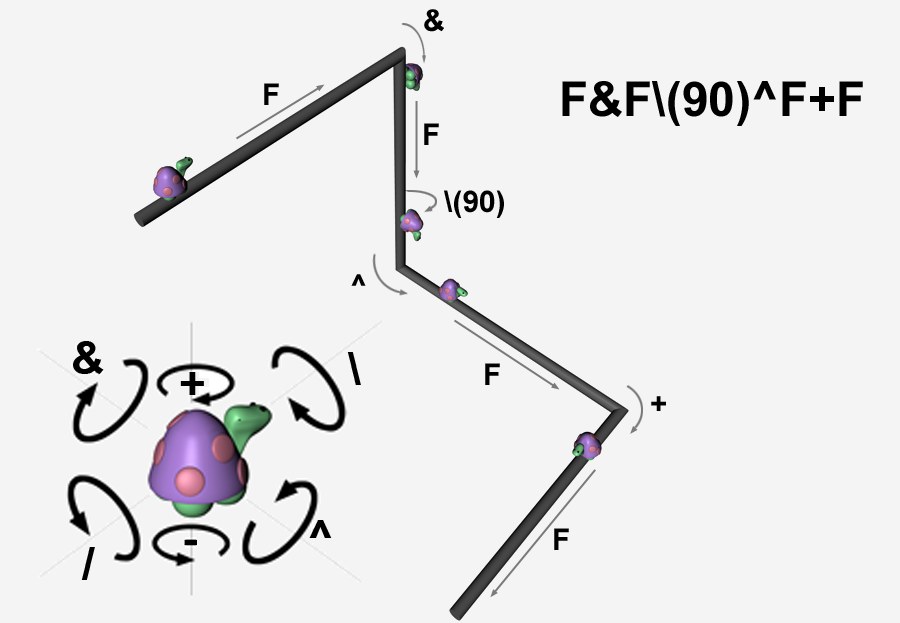Die "(90)" hinter dem "/" sind nicht unbedingt nötig, da bei keiner Spezifizierung der Standardwinkel verwendet wird.

Es ergibt sich der abgebildete Spline: Die Schildkröte trottet ein Stück vorwärts (F), dreht sich rechtwinklig um ihre Querachse (&, Standardwinkel steht auf 90°), trottet wieder ein Stück vorwärts (F), dreht sich 90° um ihre Längsachse (\ (90)), dann 90° um ihre Querachse (^) , läuft dann wieder ein Stück gerade (F), biegt dann rechts ab (+) und kriecht dann schließlich wieder ein gerades Stück nach vorne (F).

Wenn Sie auf diese Art und Weise räumliche Strukturen mit Zweigen verwenden, erhalten Sie echte Büsche und Bäume

Benutzerdaten

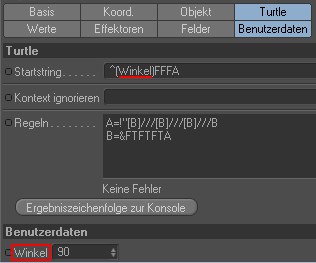
Sie können Benutzerdaten verwenden, um diese als Variablen in einer Zeichenfolge zu verwenden. Bei obiger Abbildung wurde bei den Benutzerdaten ein Winkel definiert, der dann einfach oben in Klammern für "^" (Turtle um Querachse drehen) eingesetzt wurde.

Im Variablennamen sollten keine Sonderzeichen/Leerzeichen vorkommen. Unterstriche funktionieren (z.B. zweite_laenge). Groß-Kleinschreibung wird beachtet.

Formeln

Anstatt normaler Zahlen können Sie in den Feldern auch Formeln samt einigen fest definierten Variablen eingeben (z.B. F(_growth*2). Es gibt folgende:

_total	Die Gesamtanzahl an Befehlen im aktuellen String (s.u.)
_index	Der aktuelle Befehlsindex im String (s.u.)
_growth	Der aktuelle Wachstumslevel
_level	Der aktuelle Befehlslevel (sofern zugewiesen, s.u.)
_x, _y, _z	Die aktuelle Turtle-Position im Raum.
_arg1, _arg2, _arg3, _arg4	Der erste, zweite, dritte und vierte Argumentwert (z.B. von F(1,2,3,4))
_age	Das aktuelle Befehlsalter (entspricht _growth - _level) beginnend mit 0.0.
_length	Die aktuelle Bogenlänge zwischenTurtle und MoSpline-Ursprung.
_move	Die aktuelle Standardgrößenlänge.
_tropism	Der aktuelle Tropismus.
_scale	Die aktuelle Standardgröße.
_rotate	Der aktuelle Standardwinkel.
_rnd, random	Eine Zufallszahl zwischen -1.0 und +1.0

Beispiel "Total/Index"

Angenommen Sie haben einen String F(_index)F(_index), das sind 2 Befehle, d.h. der String macht das gleiche wie F(1)F(2) (also einmal 1 und einmal 2 Einheiten vorwärts). Da "_total" die Gesamtanzahl der Befehle ist, erhalten Sie z.B. bei einer solchen Anweisung eine Spirale:

Startstring: FA

Regel: A=+(20*_index/_total)FA

Beispiel "_RND"

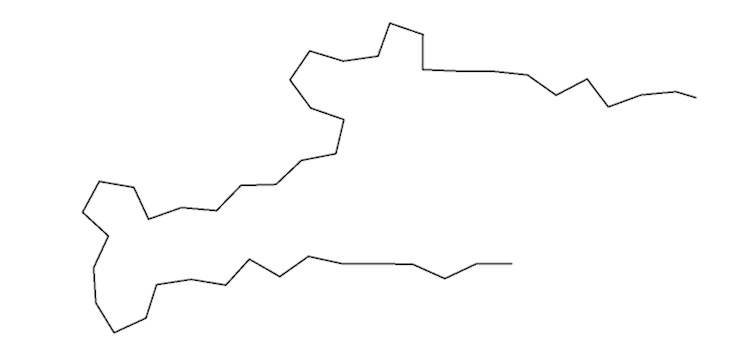
Folgende Anweisung:

Startstring: A

Regel: A=+(_rnd*90)FA

Mittels "_rnd*90" wird bei jedem Wachstumsschub ein zufälliger Winkel zwischen -90 und +90 ermittelt, d.h. es ergibt sich eine "wackelige" Linie mit zufälligen Winkelsprüngen.

Beispiel "_level"

Nehmen wir an, es gibt folgende Anweisungen:

Startstring: A

Regel: A=FA

Dann ergeben sich folgende Levelwerte (die sind hier in Klammern zur Veranschaulichung angegeben, werden aber nicht(!) angezeigt):

Wachstum = 0 : A(0)

Wachstum = 1 : F(1)A(1)

Wachstum = 2 : F(1)F(2)A(2)

Wachstum = 3 : F(1)F(2)F(3)A(3)

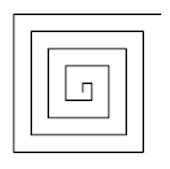
Nachdem Sie jetzt wissen, wie die "_index"-Nummerierung vorgenommen wird, betrachten Sie sich diese Anweisung:

Startstring: FA

Regel: A=+F(_level*10)A

ergibt bei 90°-Standardwinkel dann eine solche Spirale:

Beispiel "_arg"

So wie Sie F(a,b,c)=F(a*2,b*2,c*2) definieren können, um Parameter von Turtle-Befehlen (hier beispielsweise "F") einzustellen, können ebenfalls die "_arg"-Befehle verwendet werden. Diese müssen dann nicht zu Beginn erst ausgewiesen werden. F=F(_arg1*2,_arg2*2,_arg3*2) macht das gleiche, wie obige Zuweisung.

Weitergehende Syntaxvarianten

Ebenfalls möglich ist folgende Syntax:

Startstring: F(2)F(1,2)F(2,3)

Regel : F(a,b) = F(a*2,b*2)

Hiermit werden alle "F" ersetzt und überall dort in der Regel, wo sich "a" oder "b" befinden, werden existierende F-Argumente solchermaßen behandelt:

F(2*2,1*2)F(1*2,2*2)F(2*2,3*2) was logischerweise F(4,2)F(2,4)F(4,6) entspricht.

Auch solche Regelkonstrukte sind möglich:

F(a,b):(a>10)=F(a,b)+F(a/2)

Diese Regel wird beispielsweise nur angewandt, wenn der Wert des ersten Arguments größer als 10 ist.

Im folgenden Beispiel wurden beide eben beschriebenen Syntaxvarianten kombiniert, womit sich folgender interessant Effekt ergibt:

Beispiel "Früchte"

Hier wachsen mehrere Zweige gleichzeitig, wenn ein Zweig ausgewachsen ist, wird eine Kugel am Zweigende positioniert (das besorgt der Befehl "J", s. Beispiel Klon-Objekt).

Beachten Sie, wie in der ersten Regel "B(6)" definiert wird, während in der 2. Regel bei jedem Durchgang durch "B(h-1)" das Argument um "1" reduziert wird, bis die 3. Regel schließlich bei "h=0" die Kugel setzt.

Werfen Sie einen Blick auf die Konsole, um den Komplettstring zu betrachten (aber vorher auf den Button Ergebniszeichenfolge zur Konsole klicken!).

Weitere Details zu Fomeln finden Sie übrigens auch im Anhang.

Startstring

Geben Sie hier den Startstring ein. Das sind meist Ein-Buchstaben-Befehle (s. Regeln) oder Platzhalter, die im Regeln-Feld mit Inhalt gefüllt werden. Sie finden hier und auf den folgenden Seiten viele Beispiele, wie solche Startstrings aussehen können.

Kontext ignorieren

Sie können hier eine Reihe von Zeichen (Befehle) definieren, die bei Kontextregeln ignoriert werden. Beispiel:

Sie haben folgende Konstellation:

Startstring: A+B+C+D+E+F

Regeln: A<B=C

Regeln

F(a,b,c)	bewegt Turtle nach vorne, die dabei optional eine Linie der Länge a, der Dicke b und der Unterteilung c malt.
f(a)	bewegt Turtle nach vorne, dabei wird KEINE Linie gemalt (damit wird also ein Splinesegment beendet). a ist die optionale Länge.
H(a,b,c)	bewegt Turtle nach vorne, die dabei optional eine Linie der halben Länge a, der Dicke b und der Unterteilung c malt.
h(a)	bewegt Turtle nach vorne, dabei wird KEINE Linie gemalt (damit wird also ein Splinesegment beendet). a ist die optionale halbe Länge.
M(x,y,z)	bewegt und malt eine Linie. Die Turtle bewegt sich dabei in lokalen Koordinaten und dreht sich dabei selbst nicht.
m(x,y,z)	bewegt, malt dabei aber keine Linie. Die Turtle bewegt sich dabei in lokalen Koordinaten und dreht sich dabei selbst nicht.
G(a)	bewegt Turtle nach vorne, malt dabei keine Linie, beendet aber Splinesegment nicht. a ist die optionale Länge.
R	Setzt Turtle auf den Segmentstartpunkt zurück und malt dabei eine Linie (in einem Turtle-MoSpline ist ein Segment immer das, was in [] eingeschlossen ist).
r	Setzt Turtle auf den Segmentstartpunkt zurück und malt dabei keine Linie (in einem Turtle-MoSpline ist ein Segment immer das, was in [] eingeschlossen ist).
P(x,y,z)	Setzt die Turtle auf diese Koordinate und malt eine Linie.
p(x,y,z)	Setzt die Turtle auf diese Koordinate und malt keine Linie.
-(a)	Dreht Turtle gegen den Uhrzeigersinn um die Hochachse. a ist der optionale Winkel.
+(a)	Dreht Turtle im Uhrzeigersinn um die Hochachse. a ist der optionale Winkel.
&(a)	Dreht Turtle nach vorne um die Querachse. a ist der optionale Winkel.
^(a)	Dreht Turtle nach hinten um die Querachse. a ist der optionale Winkel.
/(a)	Dreht Turtle im Uhrzeigersinn um die Längsache. a ist der optionale Winkel.
\(a)	Dreht Turtle gegen Uhrzeigersinn um die Längsache. a ist der optionale Winkel.
[	Neuer Ast = neue Turtle.
]	Ast zu Ende.
{	Beginnt Polygon (s. Beispiel unten "Polygonerzeugung").
}	Beendet Polygon.
.	Hinzufügen eines Polygonpunktes (innerhalb von geschweiften Klammern für Polygone: z.B. ={.-f.+f.+f.+f} ).}
\|	Dreht die Turtle 180° um die Hochachse.
*	Dreht die Turtle 180° um die Längsachse.
%	Stutzt den Zweig ab diesem Punkt (bis zum Ende der schließenden ]-Klammer wird alles ignoriert; s. Beispiel "Zweig abschneiden").
“(a)	Multipliziert für jede Generation die Größe (MoSplinedurchmesser bei Verwendung mit Sweep-Objekt) mit dem optionalen Wert a.
!(a)	Multipliziert für jede Generation die Länge mit dem optionalen Wert a (s. Beispiel unten "Beispiel Multiplizieren/Dividieren").
;(a)	Multipliziert für jede Generation den Winkel mit dem optionalen Wert a.
_(a)	Dividiert für jede Generation die Länge durch den optionalen Wert a.
?(a)	Dividiert für jede Generation die Größe (MoSplinedurchmesser bei Verwendung mit Sweep-Objekt) durch den optionalen Wert a.
@(a)	Dividiert für jede Generation den Winkel durch den optionalen Wert a.
T(a)	Fügt Tropismus hinzu (z.B. FTFTF), d.h. jeder Splineabschnitt wird etwas in Richtung Welt-Y-Achse gebogen. Evtl. vorhandene Partikel-Modifikatoren werden ausgewertet.
$(x,y,z)	Stellt das Ende eines Upvektors dar und orientiert die Turtle demensprechend. Geben Sie hiermit einen Vektor an, in dessen Richtung die Turtle blickt.
I(a,r,g,b)	(grosses "i" vor der Klammer)
J(a,r,g,b)
K(a,r,g,b)
L(a,r,g,b)	Hiermit können per Klon-Objekt geklonte, beliebige Objekte an einem Turtle-Spline aufgereiht werden. "r,g,b" ist dabei die Farbe der Klone. a ist der Index (also die Nummer, die der Reihenfolge der unter einem Klon-Objekt befindlichen Objekte entspricht, s.u. Beispiel "Index). I, J, K, L entspricht dabei jeweils der unter "Modus" des Klon-Objekts definierten "Gruppe 1", "Gruppe 2", "Gruppe 3", "Gruppe 4". Ein Beispiel hierzu finden Sie unten unter "Beispiel Klon-Objekt".

Beispiel "Polygonerzeugung"

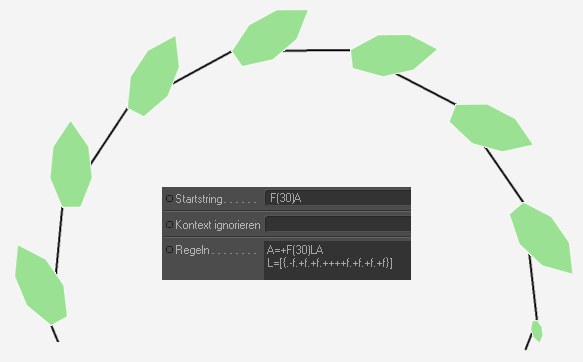
Betrachten Sie sich einmal die 2. Zeile des Regeln-Feldes:

L=[{.-f.+f.+f.++++f.+f.+f.+f}]

Innerhalb der geschweiften Klammern (diese erzeugen ein Polygon) werden eine Anzahl Polygonpunkte (jeweils eingeleitet mit einem ".") festgelegt, zwischen denen das Polygon erzeugt wird. Dadurch, dass die geschweiften Klammern zusätzlich noch in eckigen Klammer eingefasst sind, wird die Turtle nach der Blattzeichnung jeweils an den Punkt vor Beginn der Blattzeichnung zurück gesetzt.

Das ganze Blatt wird einfach einem "L" zugewiesen, womit in der darüberliegenden Regelzeile überall dort, wo ein "L" steht, ein komplettes Blatt eingefügt wird.

Beachten Sie, dass der MoSpline entweder einen Spline ODER Polygone produzieren kann. Wenn Sie beides gleichzeitig brauchen, so greifen Sie auf den Zielspline zurück.

Beispiel "Multiplizieren/Dividieren"

Wenn Sie bei den Regeln eine sich selbst ersetzende Zeichenfolge verwenden (z.B. A=F+FA) kann einer der Multiplikatoren bzw. Divisoren ", !, ;, _, ?, @ verwendet werden, um mit jeder neuen Generation den vorhandenen Wert zu verkleinern oder zu vergößern.

Beispiel "Zweig abschneiden"

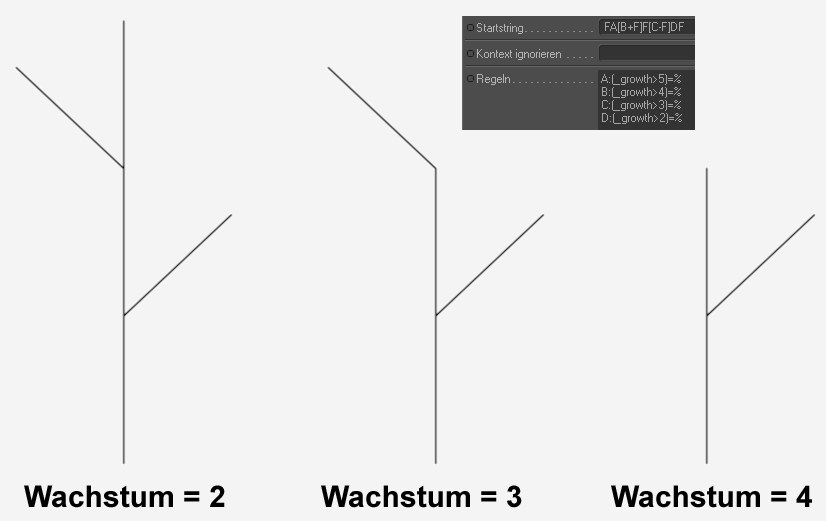
Wenn Sie sich dieses Beispiel betrachten, sind im Startstring die Platzhalter A, B, C und D verteilt. Die Regeln definieren jetzt für verschiedene Wachstum-Werte das Ersetzen der jeweiligen Platzhalter mit einem "%", das bedeutet, ab dieser Position werden im (und pro) Zweig die folgenden Zeichen weggeschnitten.

Beispiel "Klon-Objekt"

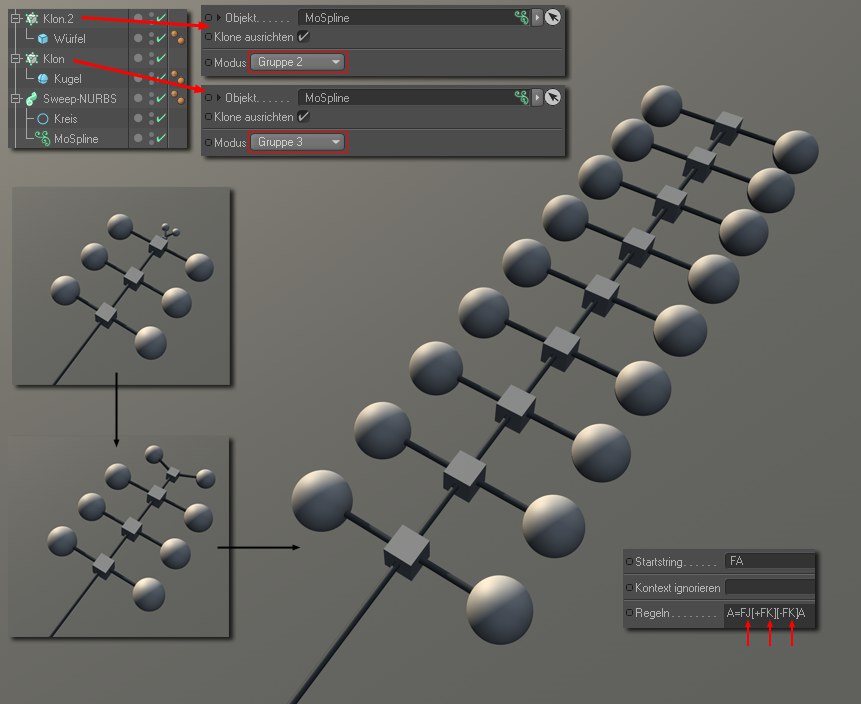Bei Animation von Wachstum kann dieses Gebilde unendlich weit "wuchern" (inkl. wachsender Klone).

Beachten Sie bei dieser Abbildung wie in der Regel "J" und "K" (man könnte auch J(1,1,1,1) bzw. K(1,1,1,1) verwenden, lässt man das Klammerargument weg, wird jeweils der Standardwert verwendet) verwendet werden, die auf die Klone eines Klon-Objekts verweisen. In den beiden Klon-Objekten muss der Modus entsprechend eingestellt werden:

I(1,1,1,1) entspricht Gruppe 1

J(1,1,1,1) entspricht Gruppe 2

K(1,1,1,1) entspricht Gruppe 3

L(1,1,1,1) entspricht Gruppe 4

Beachten Sie, dass eine Regel

Startstring: FA

Regeln: A=FX

X=J(1,1,1,1)

zwar auch funktioniert, die Klone dann aber nicht stufenlos mitwachsen, sondern einfach abrupt eingeblendet werden.

Beispiel "Index"

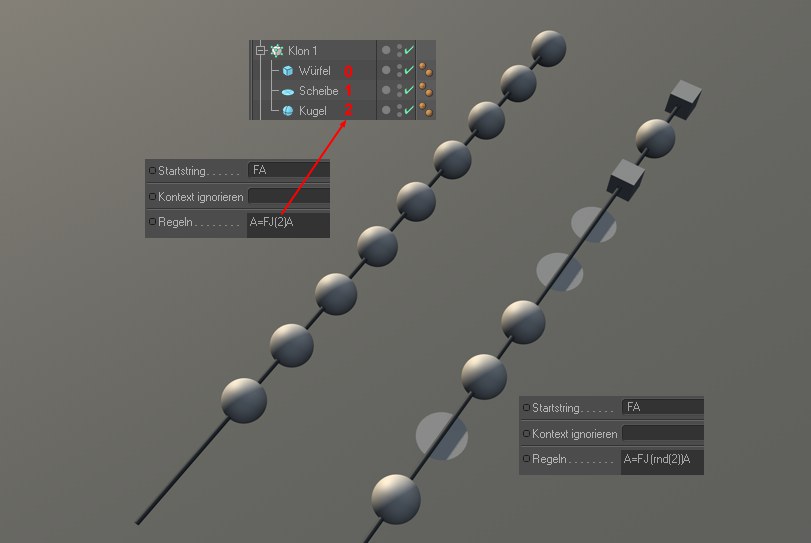
Die Objekte unter einem Klon-Objekt sind intern durchnummeriert (startend mit "0"). Wenn Sie jetzt z.B. A=FJ(2,1,1,1)A (die RGB-Werte können auch weggelassen werden) definieren, verwendet das Klon-Objekt nur das Objekt mit dem Index "2" (links die Kugel). Wenn Sie wie rechts A=J(rnd(2))A verwenden, wird jeweils eine zufällige Zahl zwischen 0 und 2 erwürfelt und dementsprechend ein zufälliger Klon platziert.

Beispiel "Zufälliges Wachstum"

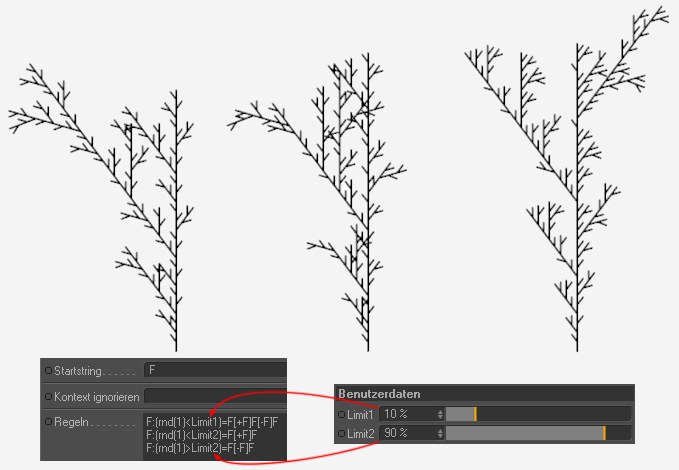Verschiedene Limits erzeugen verschiedenen Gestaltformen.

Mittels dieser Regel und variierten Benutzerdaten "Limit1" und "Limit2" (diese sollten zusammen 100% ergeben) können unterschiedliche, aber doch ähnliche "Pflanzen" erzeugt werden (sog. Stochastische L-Systeme. Die Bedingung (rnd(1)<) bzw. (rnd(1)>) entscheidet zufällig, welcher der 3 Regeln verwendet wird (mit jeweils neuem Zufall bei jeder neuen Generation (also größerem Parameter Wachstum).

Beispiel "Kontextregeln"

Sie können Regeln auch in dieser Form schreiben:

Startstring: ABC

Regel: A<B=C

Ergebnis (bei Wachstum > 1): ACC

Was passiert hier? Hier kommt es jetzt auf die Reihenfolge im Ergebnisstring an. Die Regel "A<B=C" sucht Stellen im String, wo ein "B" rechts neben einem "A" steht und ersetzt das "B" durch "C".

Schrieben Sie wiederum "A>B=C" wird das "A" links neben einem "B" durch "C" ersetzt (Ergebnis wäre "CBC").

Bei einer Regel "AB=C", kann nicht entschieden werden, welcher der beiden durch "C" ersetzt werden soll. In diesem Fall werden beide jeweils durch "C" ersetzt (Ergebnis wäre "CCC").

Resultat

Hier werden evtentuelle Syntaxfehler ausgegeben.

Ergebniszeichenfolge zur Konsole

Mittels Klick auf diesen Button, wird die wirkende Zeichenfolge unter Berücksichtigung aller Regeln und selbstverständlich des Wachstumsparameters Wachstum in der Konsole ausgegeben.

Das kann dann beispielsweise so aussehen (das ist übrigens die Zeichenfolge des Beispiels Früchte bei einem Wachstum von 4):